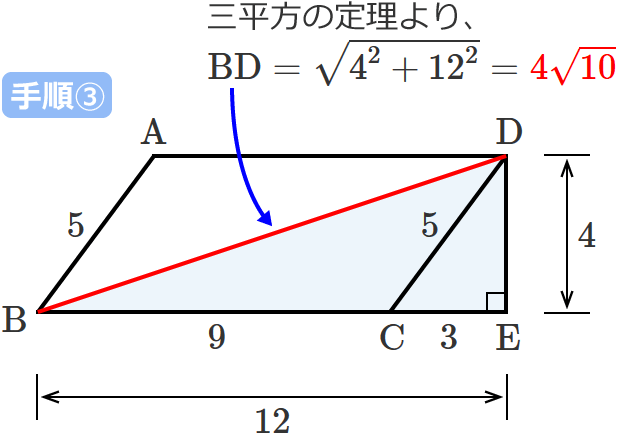
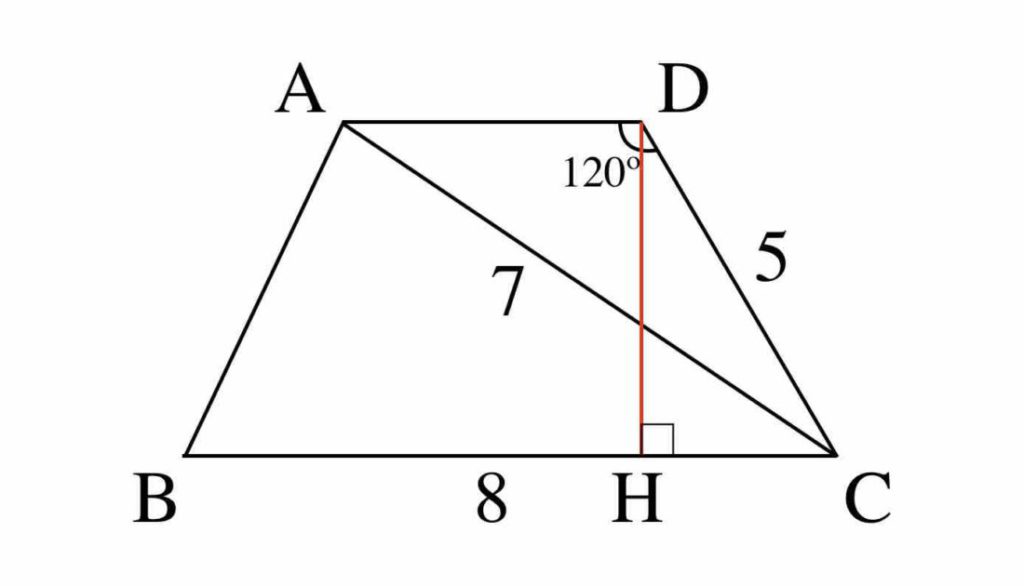
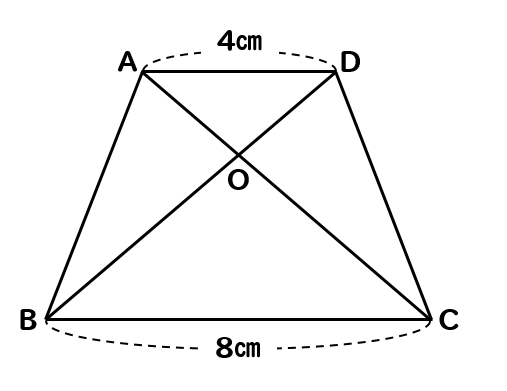
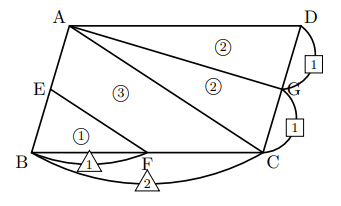
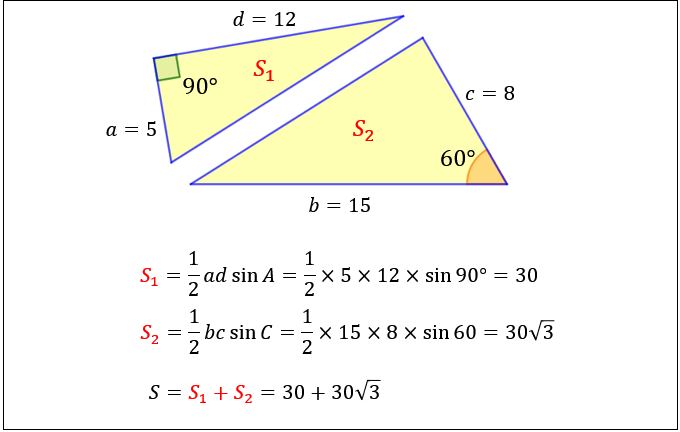
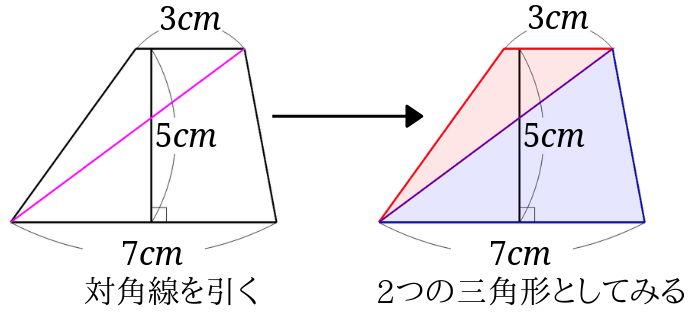
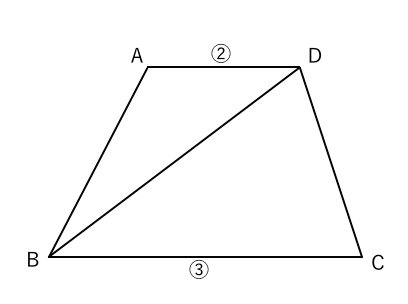
四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。
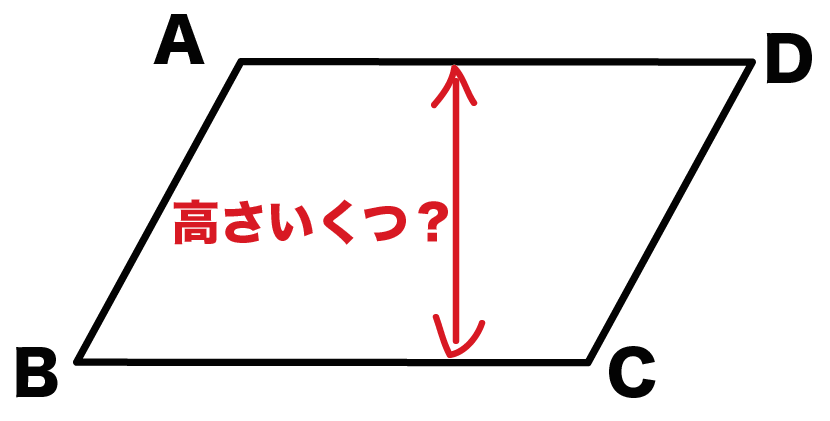
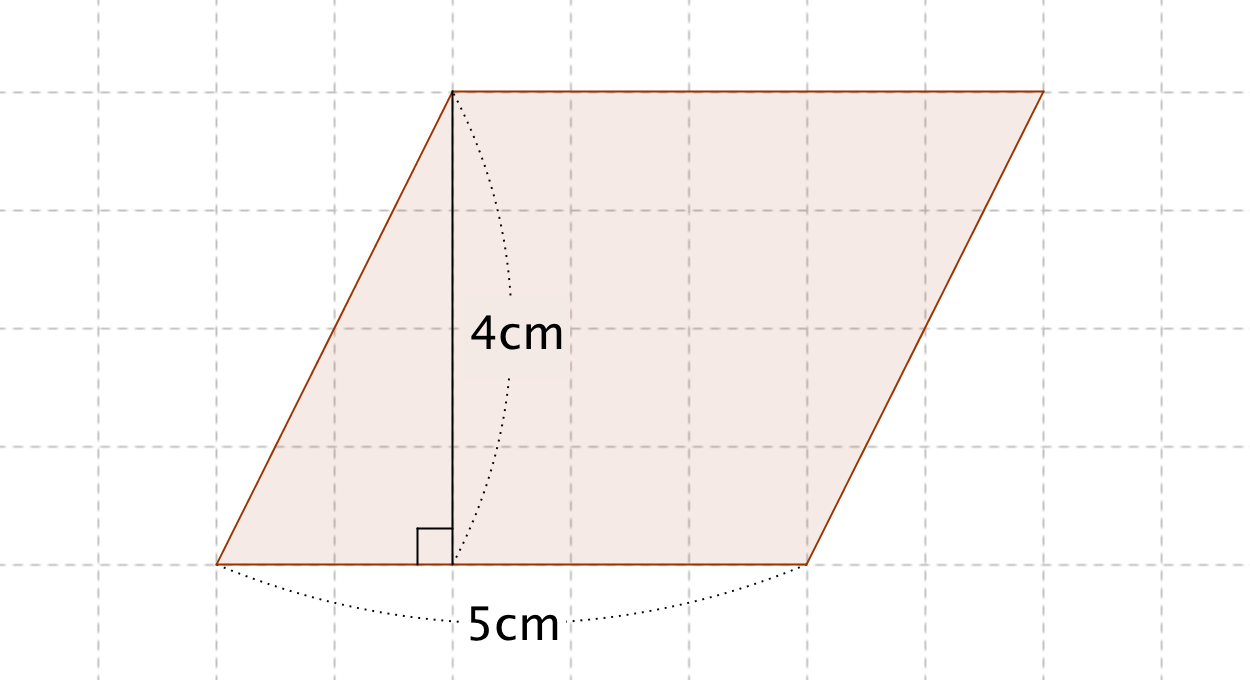
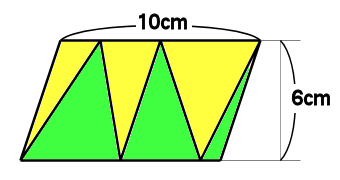
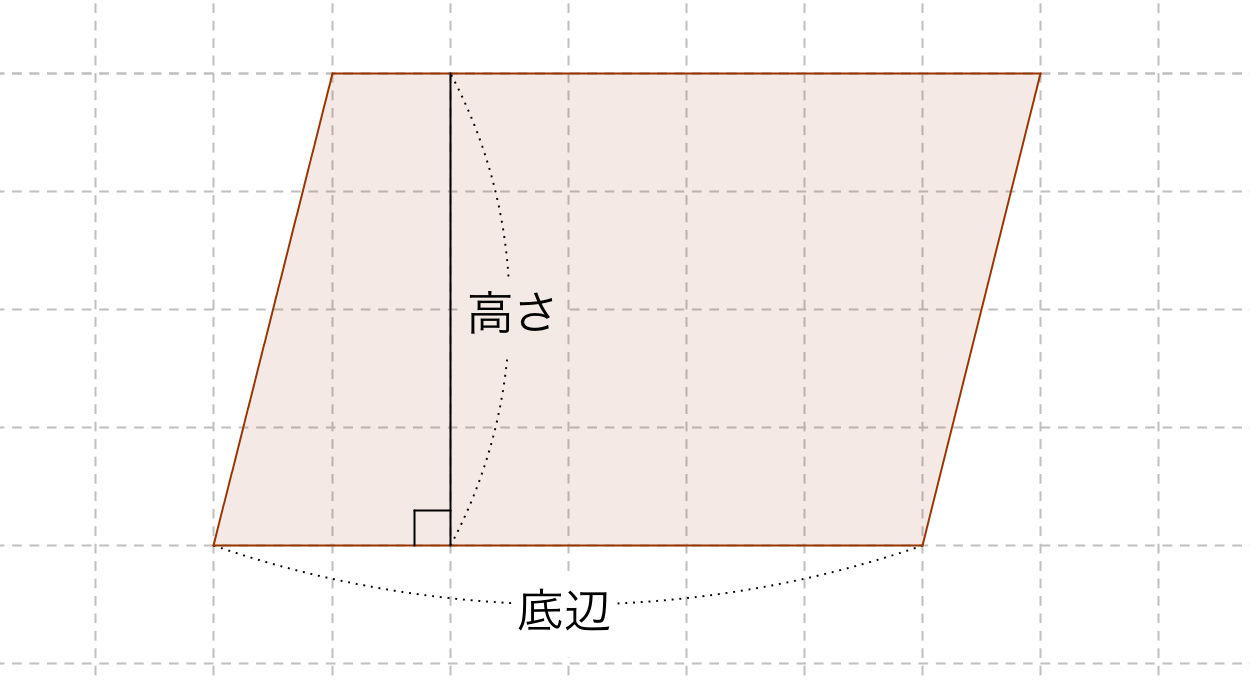
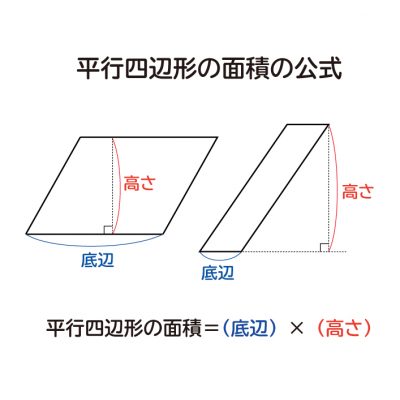
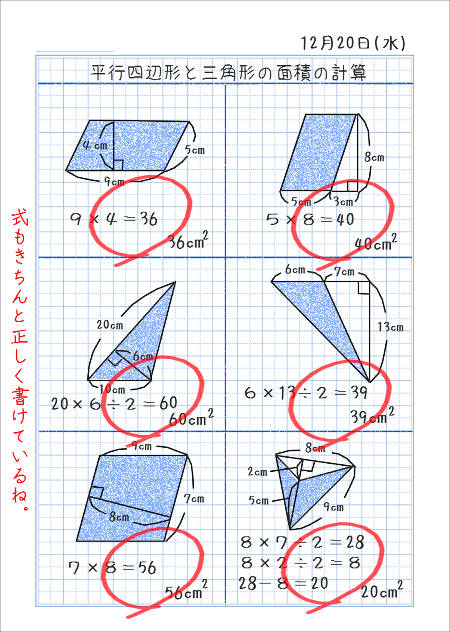
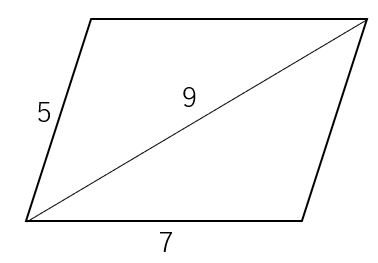
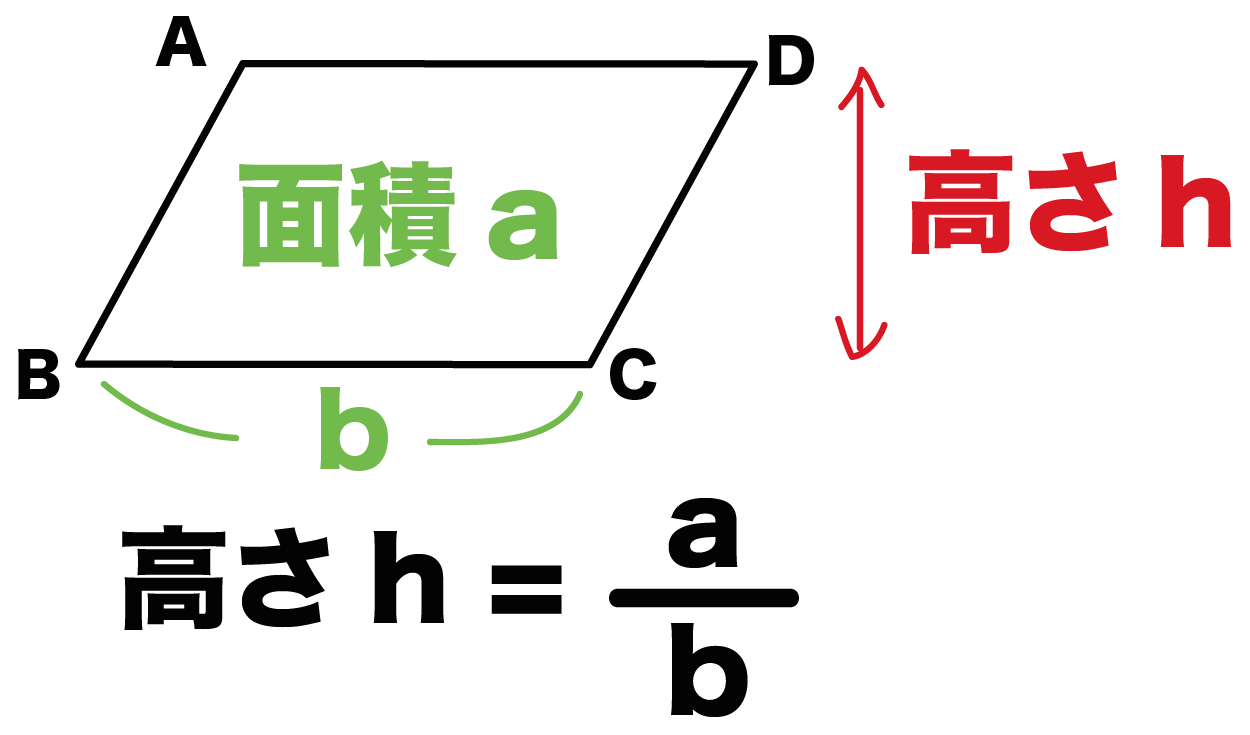
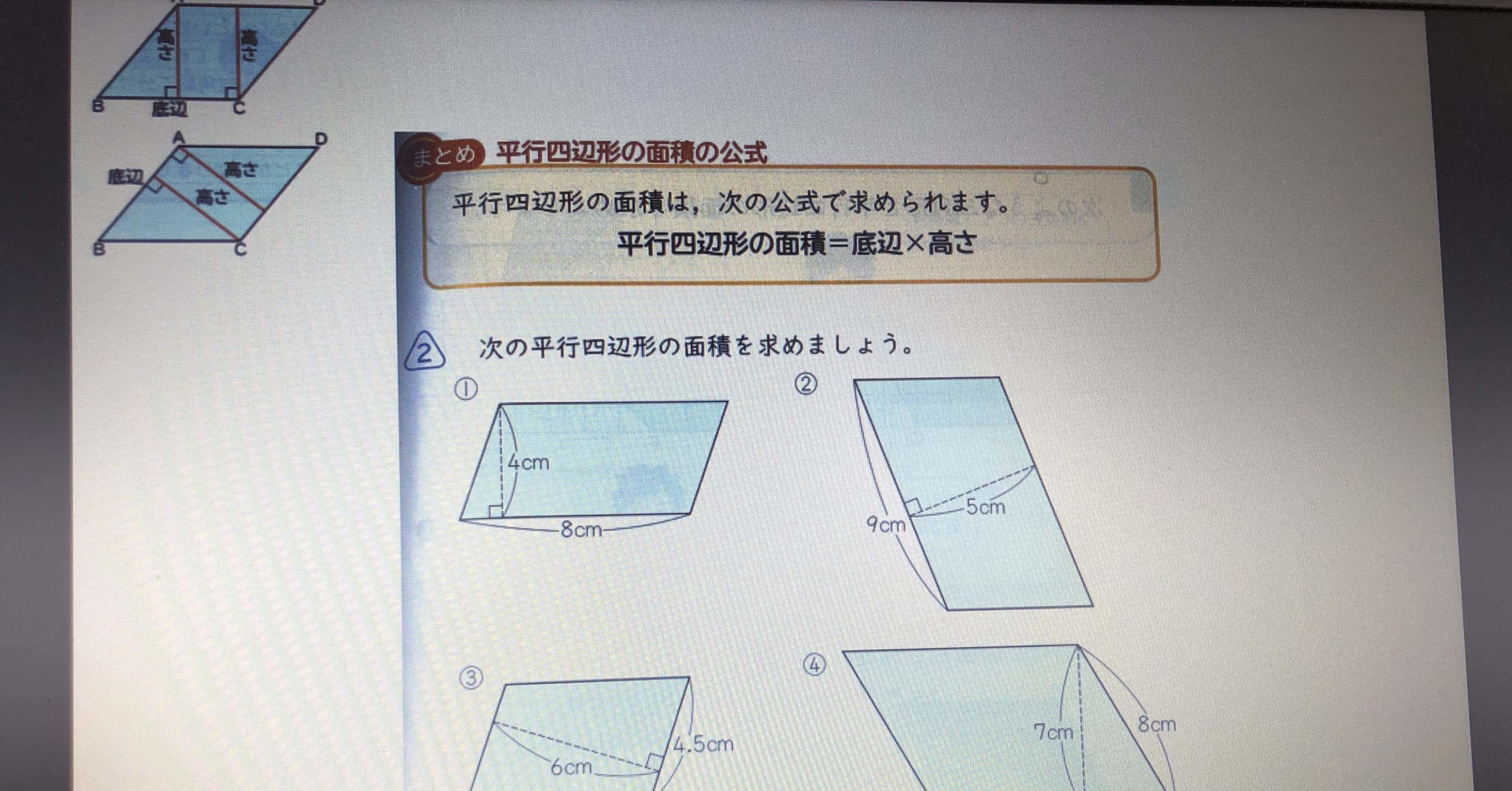
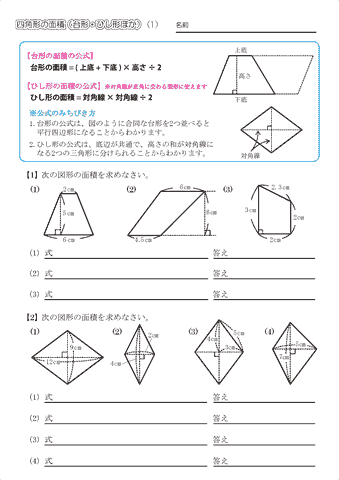
平行四辺形 三角形 面積 中学- 平行四辺形の面積の公式 平行四辺形の面積を求める公式には次の 2 通りがあります。 平行四辺形の面積の公式 平行四辺形の底辺を a 、高さを h 、斜辺を b 、底辺と斜辺のなす角を \theta とおくと、面積 S は \color {red} {S = ah} \color {red} {S = a b \sin\theta} (\text平行四辺形の面積 (2辺と間の角度) ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積
平行四辺形 三角形 面積 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  | |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 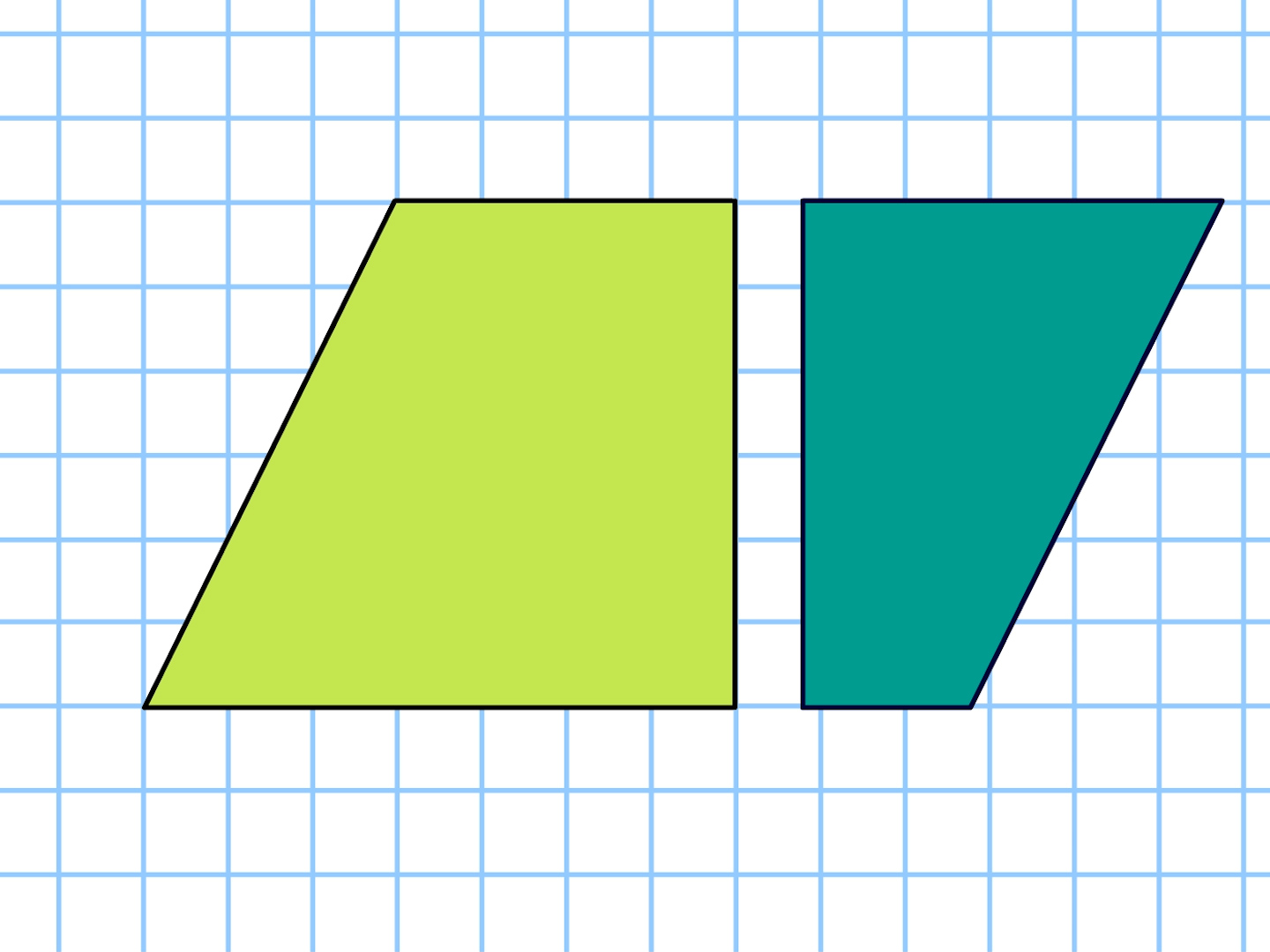 |  |
 | ||
 |  |  |
 |  | |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「平行四辺形 三角形 面積 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
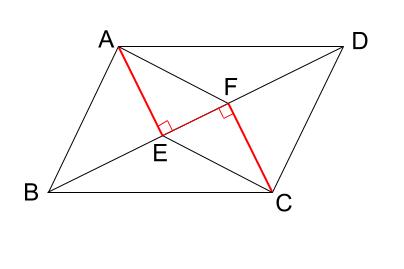 |  |
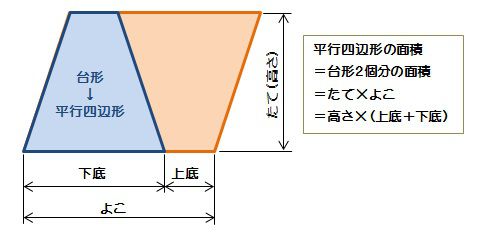
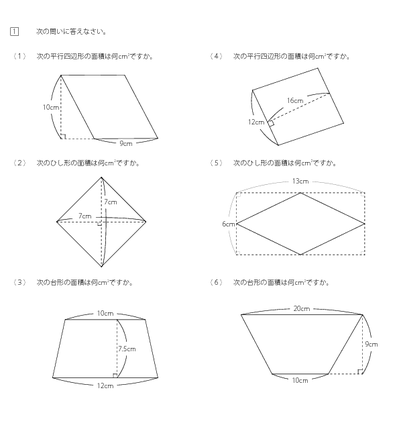
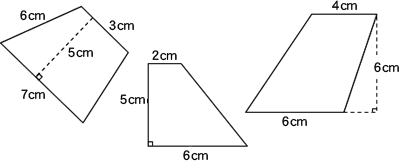
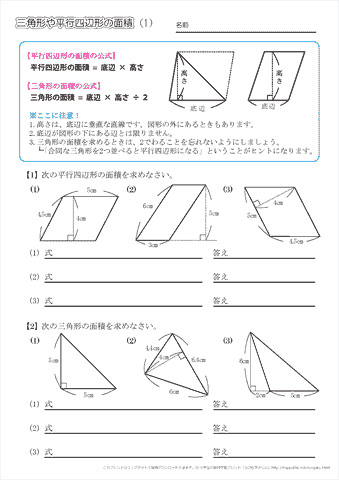
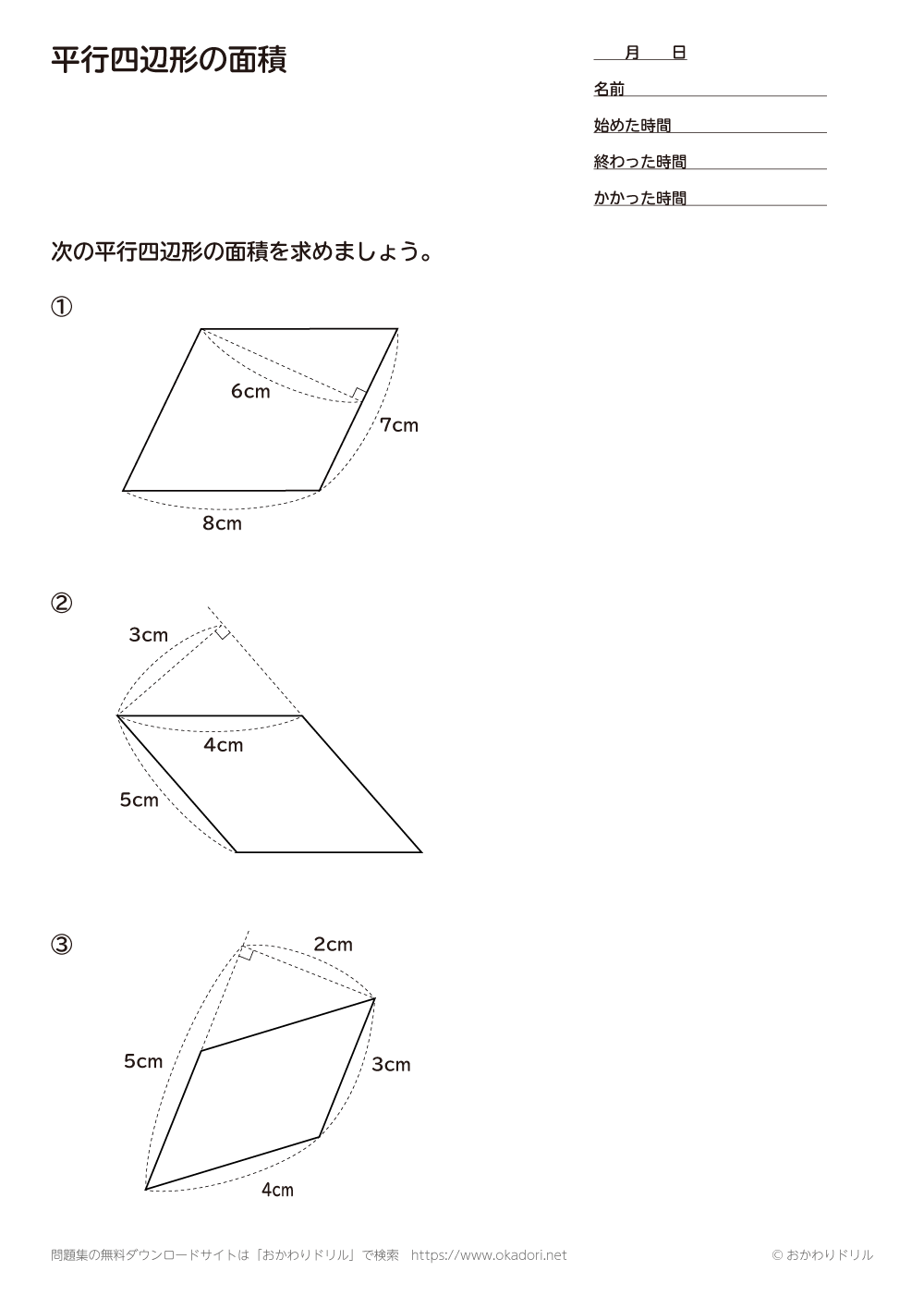
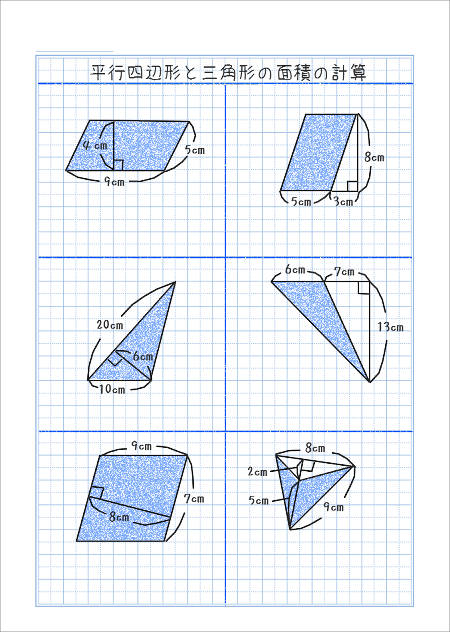
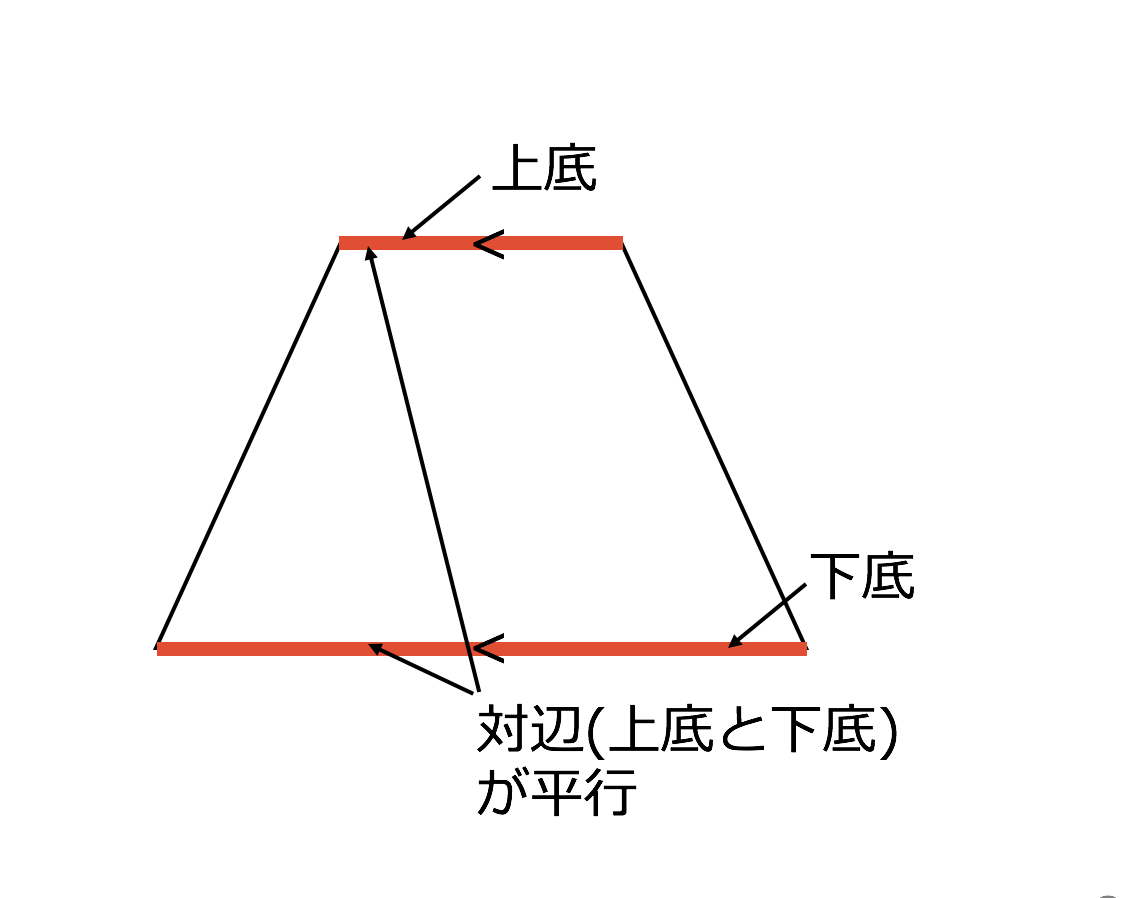
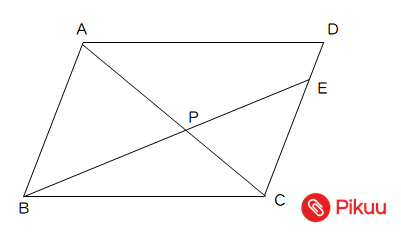
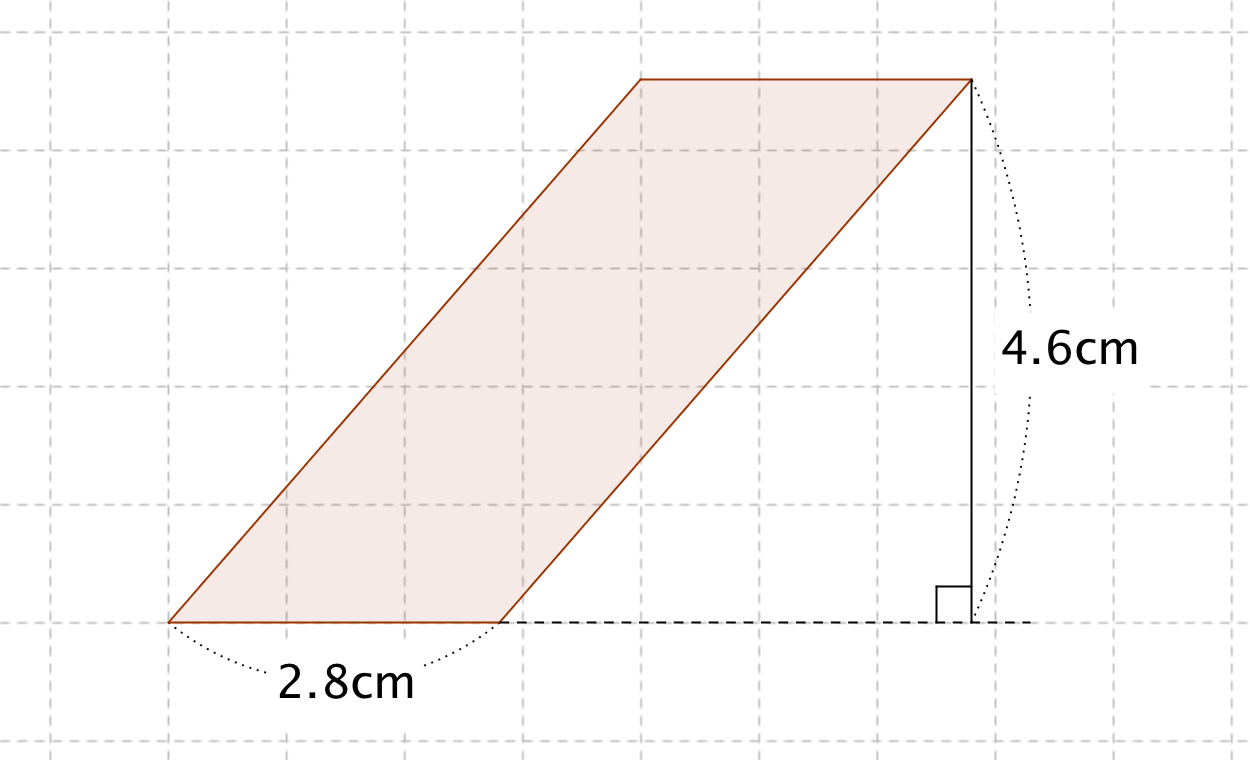
向かい合う辺がそれぞれ平行の四角形を『 平行四辺形 ( へいこうしへんけい ) 』と言いますが、平行四辺形の面積は正方形や長方形同様、簡単な計算で求めることができます。 なぜ簡単な計算で求められるのか。それは図形を変形するだけなので、図を使って説明すれば小学生でもすぐにア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 〔算数的活動〕(1)イ 三角形、平行四辺形、ひし形及び台形の面積の求め方を、具体物を用いたり、 言葉、数、式、図を用いたりして考え、説明する活動
Incoming Term: 平行四辺形 三角形 面積, 平行四辺形 三角形 面積 何倍, 平行四辺形 三角形 面積比, 平行四辺形 三角形 面積 中学, 平行四辺形 対角線 三角形 面積,




0 件のコメント:
コメントを投稿