
計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
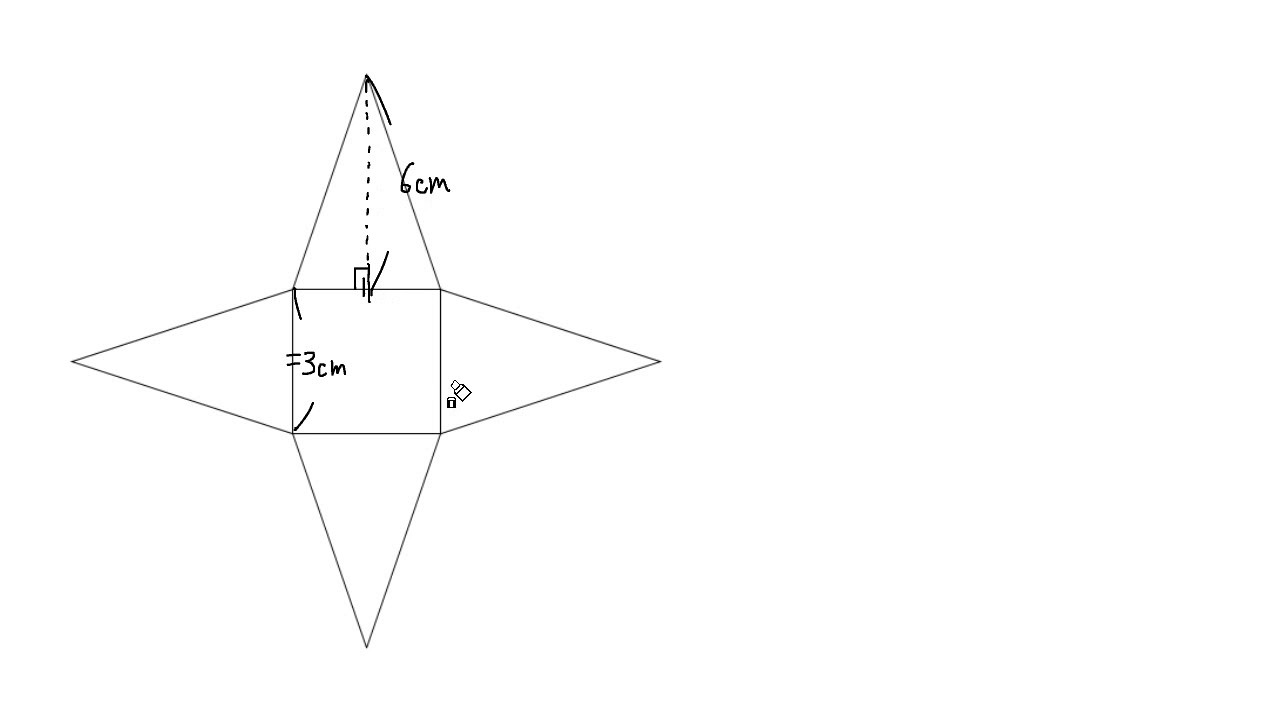
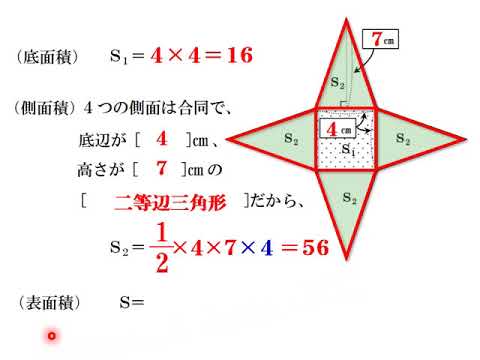
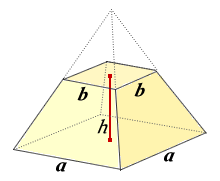
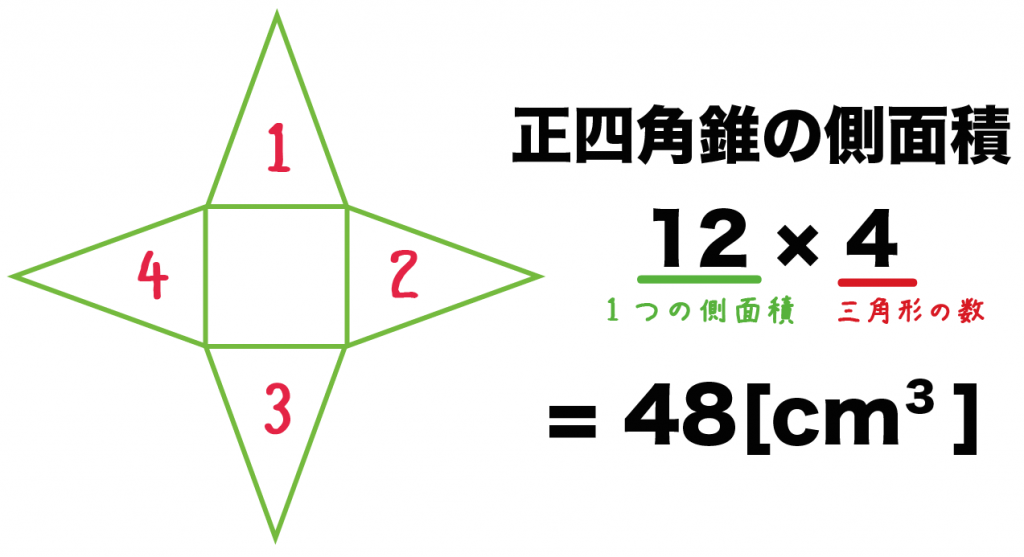
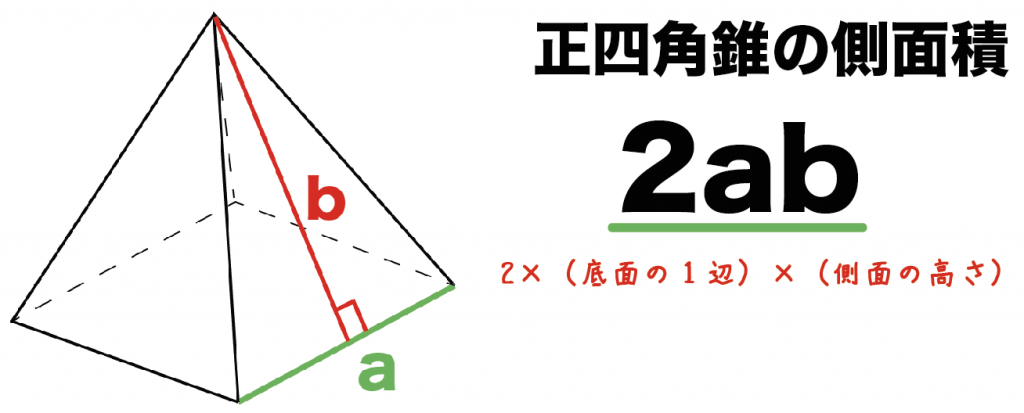
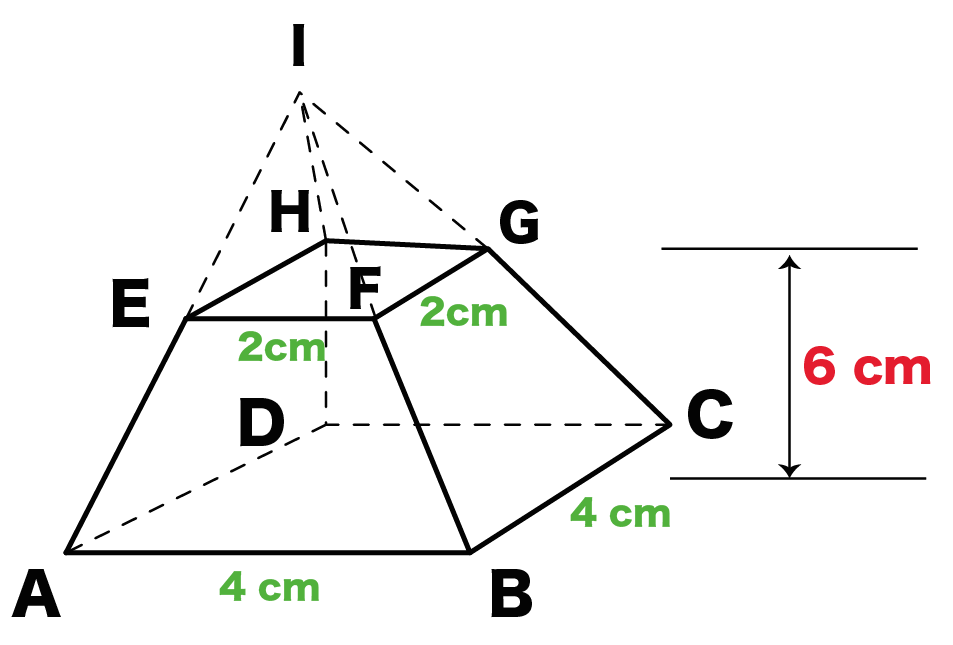
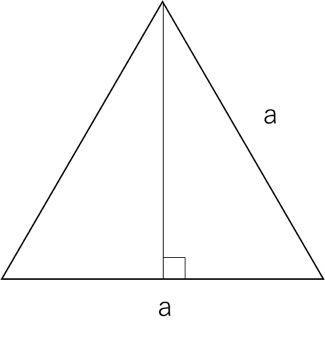
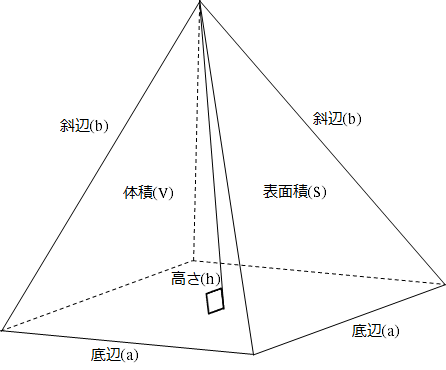
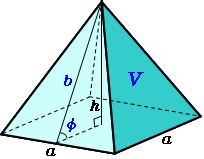
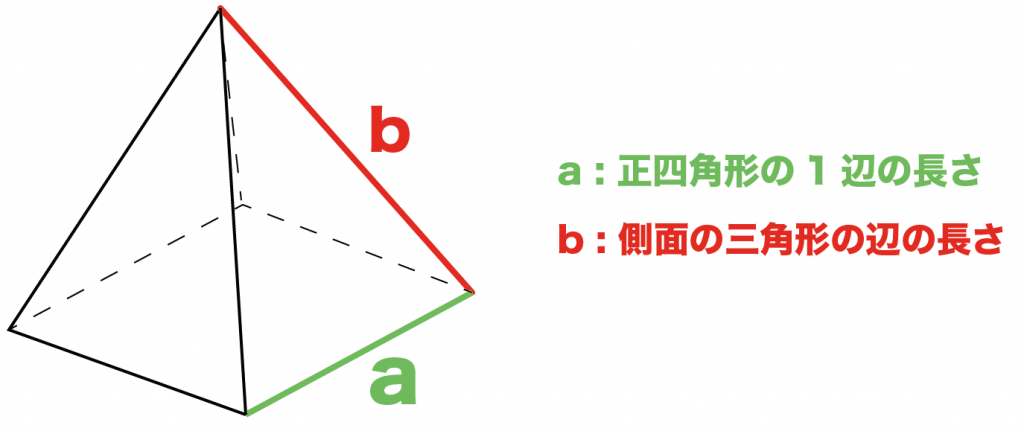
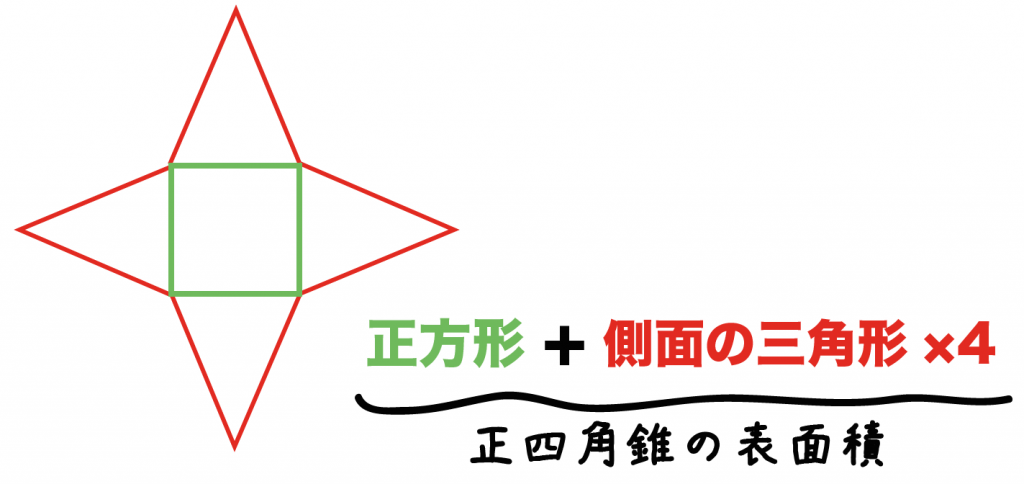
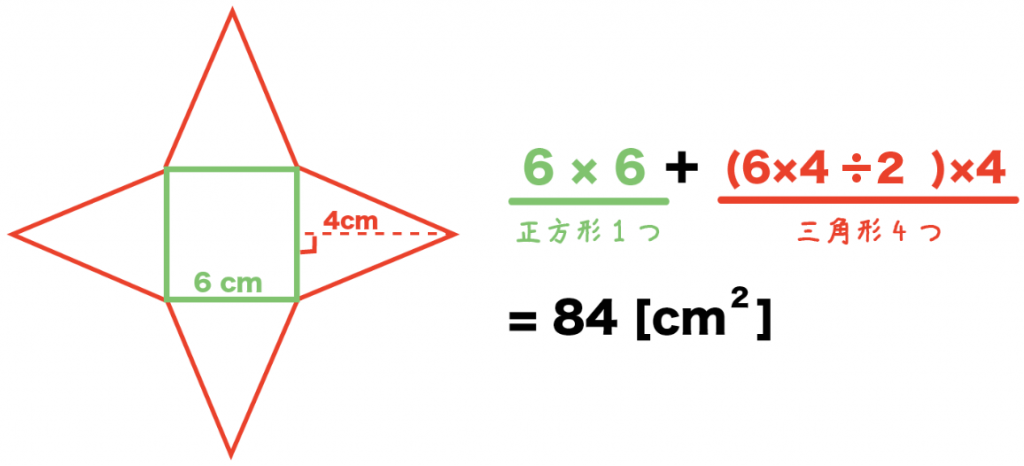
つまり、四角錐の表面積とは次のように求めることができます。 四角錐の表面積=底面積 側面積(三角形 つ分) では、実際に問題を解いてみましょう。 次の四角錐の表面積を求めなさい。 (底面は正方形) 展開図を書いて、側面積と底面積を求める そんな正四角錐の表面積は (底面の正方形)+(側面の三角形)×4 で求めることができるよ^^ だって、正四角錐の展開図が「正方形1つ」と「三角形4つ」で成り立っているからね^^ つま
正四角錐 表面積
正四角錐 表面積-空間図形の総合問題1 立方体・直方体の対角線や、正四面体・正八面体の体積・表面積について学習します。 正四角錐 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。

正四角錐側面 Natashaho
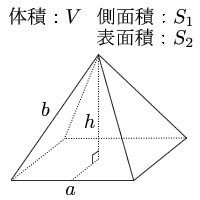
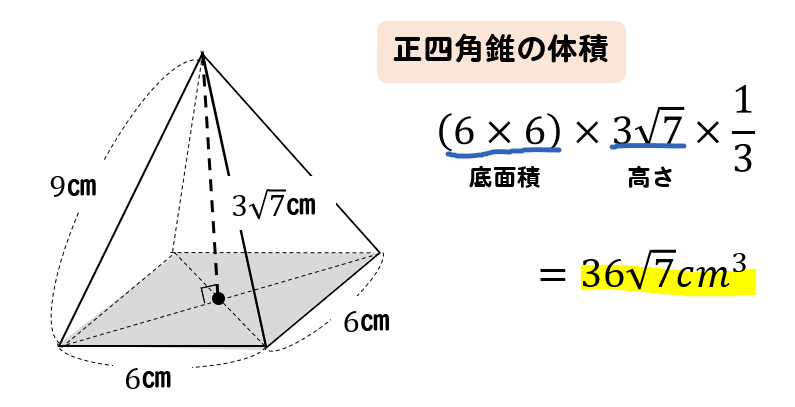
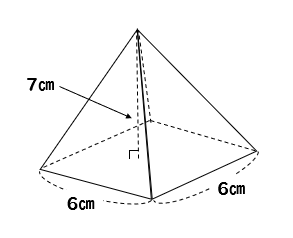
底辺の1辺の長さaが2、高さhが3の正四角錐の体積・表面積・斜辺の長さ 体積 V:4 側面積 S 1 : 表面積 S 2 : 斜辺の長さ b:位置関係2 直線の位置関係/面と直線の位置関係/角柱・角錐の体積/立体の切断など/ 円柱と円錐の体積 /円柱と円錐の表面積/球の体積・表面積/展開図/投影図/ FdData 入試製品版のご案内 FdData 入試ホームページ よって、一辺4の正三角形の面積を4倍すれば、求めたい表面積が出てくることになります。 (表面積)=(一辺が4の正三角形の面積)×4 よって、\(表面積)=4\sqrt{ 3 }×4=\style{ colorred;
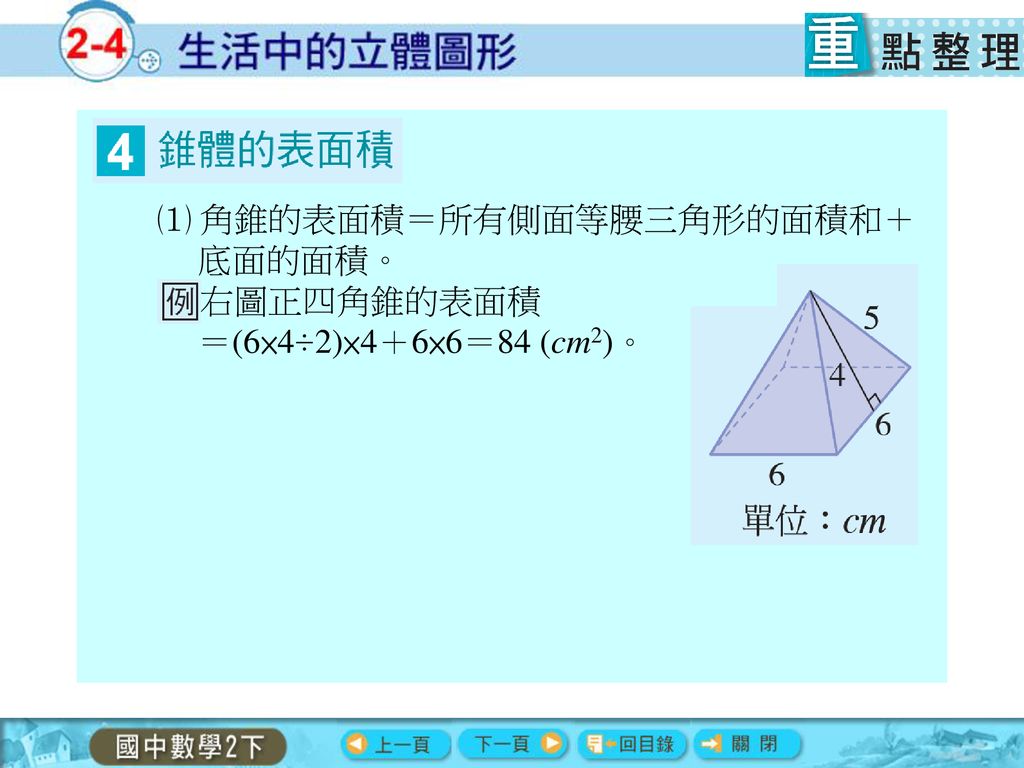
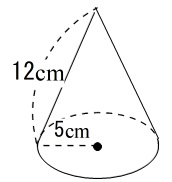
四角錐の表面積を求めるには、頂点から底面の一辺への垂線の長さが必要です 🔊 Play The volume of a cone to multiply onethird by the area of the base by the height 円錐の体積は、底面の円の面積に高さと3分の1を掛けたものになります 正四面体の表面積 \(S = \sqrt{3} a^2\) より、 \(\sqrt{3} (2\sqrt{3})^2 = 12\sqrt{3}\) 答え: \(12\sqrt{3} \, \mathrm{cm^2}\) (2) 正四面体の体積 \(\displaystyle V = \frac{\sqrt{2}}{12} a^3\) より、 \(\displaystyle \frac{\sqrt{2}}{12} (2\sqrt{3})^3 = 2\sqrt{6}\) 答え: \(2\sqrt{6} \, \mathrm{cm^3}\)1辺の長さaが1の正四面体の体積・表面積 体積 V: 表面積 S: 体積・表面積の計算 ・ 立方体の体積・表面積 ・ 立方体の体積から1辺 ・ 立方体の表面積から1辺 ・ 直方体の体積・表面積 ・ 直方体の1辺・表面積
正四角錐 表面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
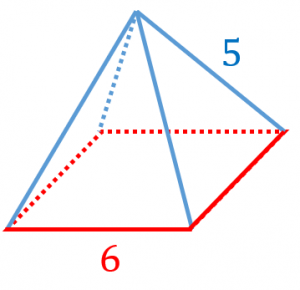
 |  |  |
 | ||
 |  | |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 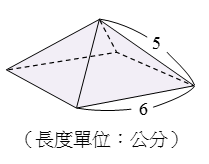 | |
 | ||
 | ||
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「正四角錐 表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 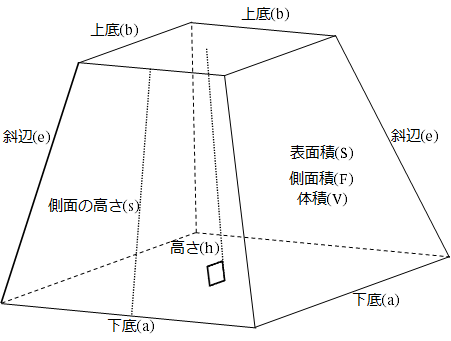 |
 |  |
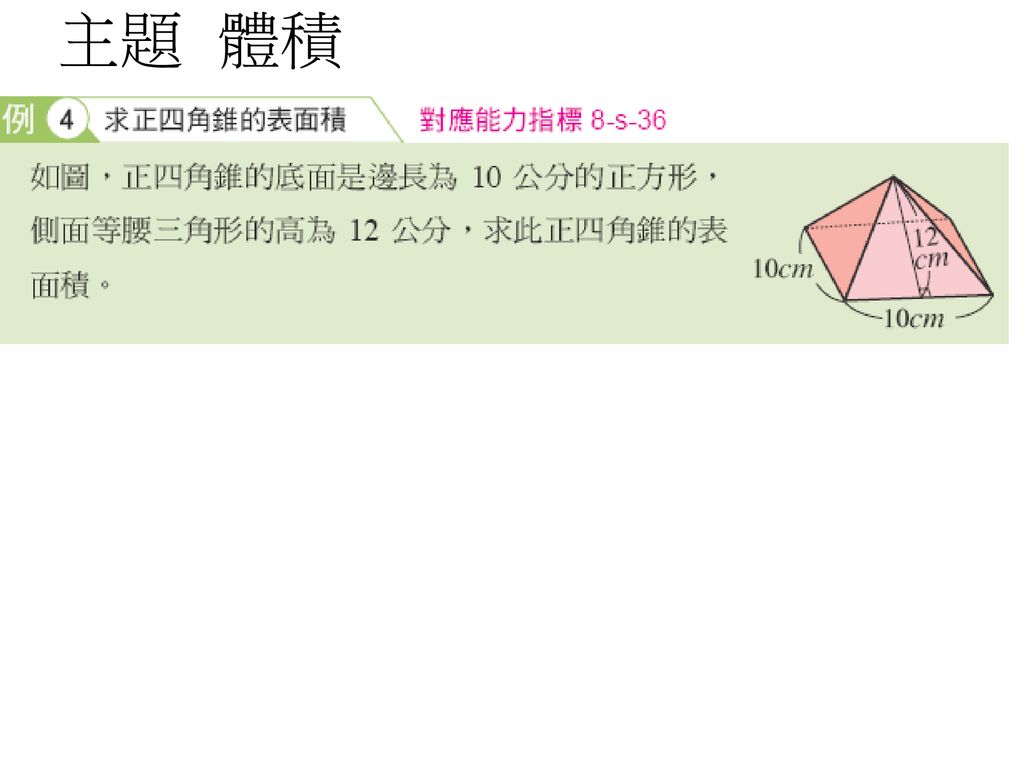
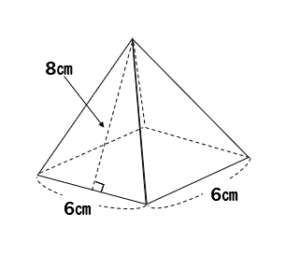
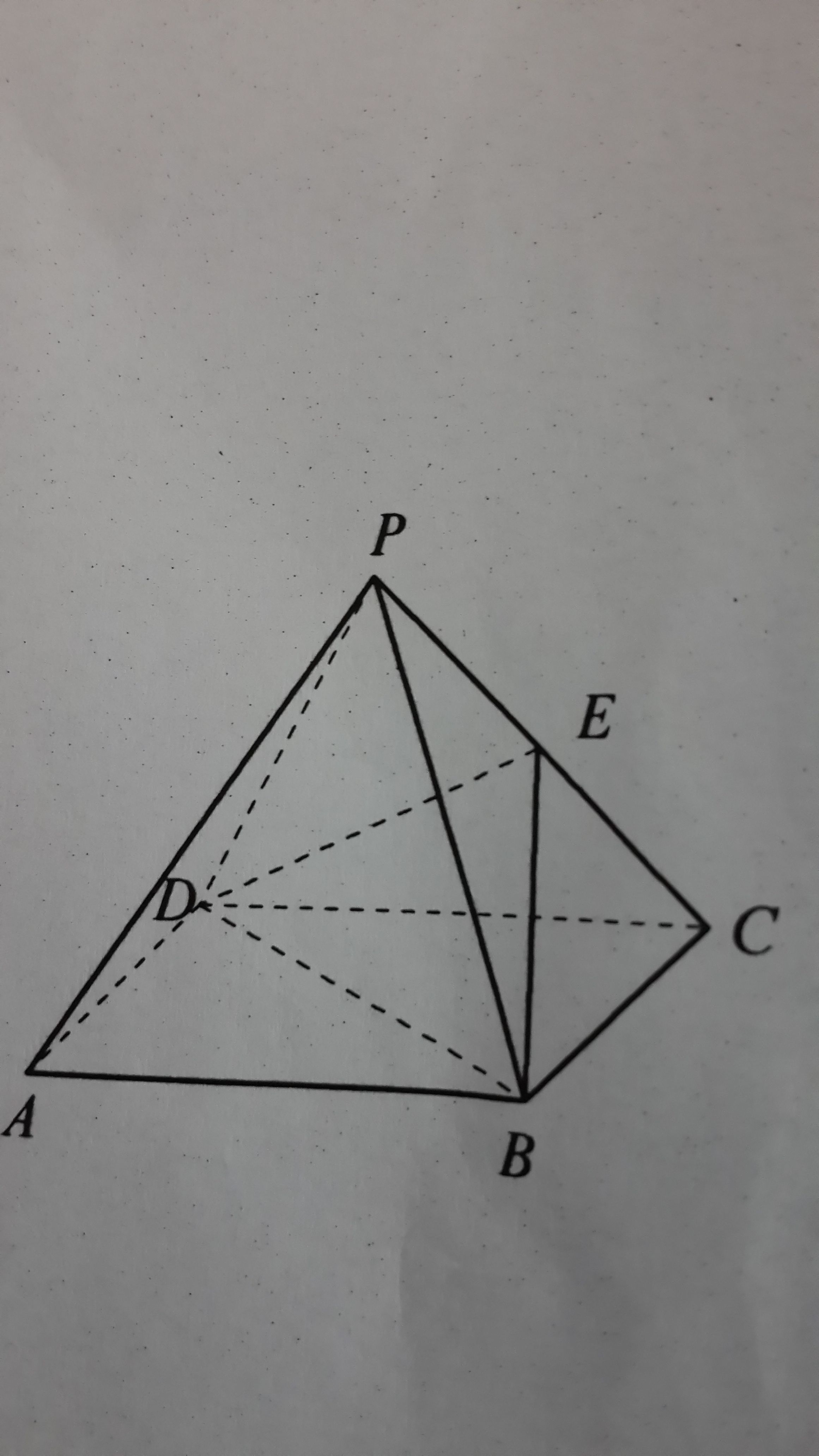
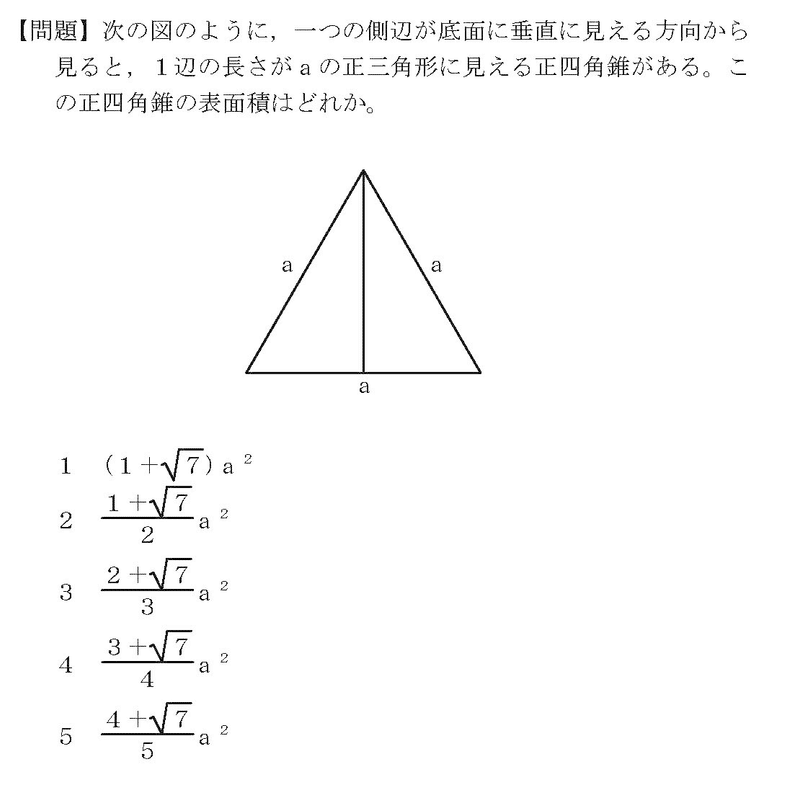
る正四角錐の表面積を求め たい。このとき、次の問い に答えなさい。 が8cmの二等辺三角形なので、側面積は、 (1) この正四角錐の底面積を求めなさい。 側面の (2) この正四角錐の側面積を求めなさい。 2 (3) この正四角錐の表面積を求めなさい。 数学 四面体のうちで、周囲の面積が一定のものの中で、体積が最大のものは 正四面体 この証明を教えてください。





0 件のコメント:
コメントを投稿