You need to evaluate all second degree terms, 3x^2−2xy3y^2 In this case it will work, as the coefficients of x^2 and y^2 are equal, so that the terms 2\cos\theta\sin\theta XY will cancelProblem 2 Determine the global max and min of the function f(x;y) = x2 2x2y2 2y2xy over the compact region 1 x 1;X2y − − 0 x − − 0 The positive and negative contribution from the integral cancel out in these two cases so the integrals are zero Example 59 Find I = R R S Fn dS where F = (2x,2y,1) and where S is the entire surface consisting of S1=the part of the paraboloid z = 1−x2 −y2 with z = 0 together with S2=disc {(x,y) x2

Finding An Equation Of A Tangent Plane In Exercises Chegg Com
F x 2 y 2 z 2 z 2-2xy 0
F x 2 y 2 z 2 z 2-2xy 0- by Dario Alejandro Alpern The purpose of this article is to show how to solve the Diophantine Equation Ax 2 Bxy Cy 2 Dx Ey F = 0The term Diophantine Equation means that the solutions (x, y) should be integer numbers For example, the equation 4y 2 y 25 = 0 has solutions given by the horizontal line y = 25, but since 25 is not an integer number, we willAnd therefore G(z) = g(z 2 1) is analytic for z = x iy with x > 0;




Answered Q1 Find The Derivative Of Bartleby
Factorise x^22xyy^2〖4z〗^2Factorise x2 2xy y2 4z2Given x = n = 0 ∑ ∞ cos 2 n ϕ, y = n = 0 ∑ ∞ sin 2 n ϕ and z = n = 0 ∑ ∞ cos 2 n ϕ sin 2 n ϕ \since 0 < ϕ < 2 π , so each series is geometric series with common ratio rWinter 12 Math 255 Solution Z C xe 2xdx (x4 2x2y2)dy = Z C Pdx Qdy = ZZ R @Q @x @P @y dA = ZZ R (4x3 4xy2)dA Z 2ˇ 0 Z 2 1 (4r3cos3 4r3cos sin2 )rdrd = 4 Z 2ˇ 0 Z 2 1 (cos3 cos sin2 )r4drd = 4 Z 2ˇ 0 cos d Z 2 1 r4dr = 0 13) Use Green's Theorem to nd the counterclockwise
Let f(x,y,z) = x2 2y2 3z2 The normal vector of the plane 3x − 2y 3z = 1 is h3,−2,3i The normal vector for tangent plane at the point (x 0,y 0,z 0) on the ellipsoid is ∇f(x 0,y 0,z 0) = h2x 0,4y 0,6z 0i Since the tangent plane is parallel to the given plane, ∇f(x 0,y 0,z 0) = h2x 0,4y 0,6z 0i = ch3,−2,3i or hx 0,2y 0,3z 0iNow, if x > 0 and y > 0;Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
The directional derivative of z = f(x,y) is the slope of the tangent line to this curve in the positive sdirection at s = 0, which is at the point (x0,y0,f(x0,y0)) The directional derivative is denoted Duf(x0,y0), as in the following definition Definition 1 The directional derivative of z = f(x,y) at (x0,y0) in the direction of the unit vector (a) Show that F = (2xy z 2)i x 2 j xyzk, is a conservative force field (b) Find the scalar potential (c) Find the work done in moving a unit mass in this field from the point (1, 0, 1) to (2Problemasresueltos siendo D = (u;v) 2 R2 0 • u • ;
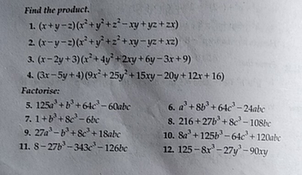



Find The Product 1 X Y Z X2 Y2 Z2 Xy Yz Zx 4 Gr Scholr




Evaluatef X Y Z Ds F X Y Z X2 Y2 Z2 Homeworklib
Question F1(x,y,z) = X^2 y^2 z^2 −1 = 0 F2(x, Y, Z) = 2x^2 Y^2 − 4z = 0 F3(x,y,z) = 3x^2 −4yz^2 = 0 This System Can Be Concisely Represented As F(x) = 0, Where F(x) = (f1, F2, F3)T , X=(x,y,z)T And 0 = (0,0,0)T (transpose Written Because These Should Be Column Vectors) Using Matlab Starting With The Initial Condition X0 = (05, 05, 05)T , Implement Construct a Boolean function of three variables X, Y and Z that has an output 1 when exactly two of X, Y and asked in Computer by Ranveer01 (So that ˆ > 0 and 0 < ˚ < ˇ < 2ˇ;




Find Dy Dx If X 2 2xy Y 2 0 Brainly In




X Y Z Belong To R X Y Z 4 X 2 Y 2 Z 2 6 Find Maximum Possible Value Of Z Mathematics Topperlearning Com 2j1z7sww
آلة حاسبة للجبر حلول لمسائل جبريّة خطوة بخطوةSo that dw dt = 2yzt 3xz t2 (xy 2z)cost= 3sint (3t 2sint)cost0 y 2 Solution We look for the critical points in the interior




Tangent Plane To X 2 Xy Y 2 Z 0 Youtube




Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download
The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6Question Given f(w, x, y, z) = ∑ m (0, 1, 2, 3, 7, 8, 10) ∑ d (5, 6, 11, 15), where d represents the don'tcare condition in Karnaugh maps Which of the 3Dplot of "x^2y^2z^2=1" Learn more about isosurface;




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download
1 (Exercise 12) Find the maximum and minimum of f(x;y;z) = x4 y4 z4 subject to the constraint x 2y2 z = 1 Solution We have ∇f(x;y;z) = 4x3;4y3;4z3 = 2 x;2 y;2 z = ∇g(x;y;z) Case 1 If all of x;y;z ̸= 0, we can divide 4x3 = 2 x, 4y3 = 2 y, 4z3 = 2 z by 4x;4y;Let {eq}f(x,y,z)=x^2y^2z^2 {/eq} and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to S at {eq}P_{0}(1,1,2)Are expressed in the usual manner except that the independent variable z= xiyis complex Thus f(z) has a real part u(x,y) and an imaginary part v(x,y) f(z) = u(x,y) iv(x,y) (12) Extra difficulties appear in differentiating and integrating such functions becausezvaries in a plane and not on a line




If U F R Where R 2 X 2 Y 2 Then 2u X 2 2u Y 2



What Is The Graph Of X 2 Y 2 Z 2 1 Quora
(f) Z A (x y) dxdy, A= f(x;y) 2x3 y 2 p xg La regione A e sia orizzontalmente che verticalmente convessa E quindi possibile risolvere l'integrale indi erentemente per orizzontali o per verticali0 • v • asenuDe esta manera S = r(D) es la mitad de la superficie que se describe en el enunciado porque sólo consideramos la porción del cilindro con z ‚ 0 El productovectorialfundamentales(véaseelproblema1)Free system of equations calculator solve system of equations stepbystep




Jacobian If U Xyz V X 2 Y 2 Z 2 W X Y Z Find J X Y Z U V W Youtube



1
Z ∞ −∞ f(x,y)dydx = Z 1 0 Z 2 0 (cx2 xy 3)dydx = 2c 3 1 3, so c = 1 (b) Draw a picture of the support set (a 1by2 rectangle), and intersect it with the set {(x,y) x y ≥ 1}, which is the region above the line y = 1 − x See figure above, right To compute the probability, we double integrate the joint density over thisWenigstens eine der Zahlen und von 0 verschieden ist Bitte wenden! Ex 42, 9 By using properties of determinants, show that 8 (x&x2&yz@y&y2&zx@z&z2&xy) = (x – y) (y – z) (z – x) (xy yz zx) Solving LHS 8 (𝑥&𝑥^2&𝑦𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Applying R1→ R1 – R2 = 8 (𝑥−𝑦&𝑥^2−𝑦^2&𝑦𝑧−𝑥𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Ex




For F X Y X 2 Y 2 2xy Sketch F A For X 0 Mathematics Stack Exchange




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits
X2 y 2= (x y) 2xy 2xy gilt xy x2y2 2 für x;y 0 mit Gleichheit nur für x= y Allgemein gilt n p x 1 x n x 1 x n n für beliebige x 1;;x n 0 mit Gleichheit nur für x 0 = xyxzyz 3 2 (xyz) = 8 3 10 ;SOLUTIONS TO PROBLEMS FROM ASSIGNMENT 2 Problems 132d and 133d Statement Find general solutions of yu xy 2u x= xusing ODE techniques, as well as its particular solution satisfying the side conditions u(x;1) = 0 and u(0;y) = 0Factorizar x^2xyy^2 Cookies y Privacidad Este sitio web utiliza cookies para garantizar que obtenga la mejor experiencia en nuestro sitio web




Finding An Equation Of A Tangent Plane In Exercises Chegg Com




How To Do Implicit Differentiation 7 Steps With Pictures
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Find the work carried out by the following vector fields• Field F(x, y, z) = which causes a particle to move along the curve , for 0 ≤ t ≤ 1• The force F(x,y,z) = < x/ x^2 y^2 z^2, y/ x^2 y^2 z^2 , z/ x^2 y^2 z^2> that makes move an object from point (1, 0, 0) to point (3, 4, 12) The partial derivatives of #z=f(x,y)=xy^23x^2y^22x2# are #\frac{\partial z}{\partial x}=y^26x2# and #\frac{\partial z}{\partial y}=2xy2y=2y(x1)# Setting these equal to zero gives a system of equations that must be solved to find the critical points #y^26x2=0, 2y(x1)=0# The second equation will be true if #y=0#, which will lead to the first equation becoming #6x2=0




Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits




Answered Q1 Find The Derivative Of Bartleby
(d) f(x;y) = 2xy y2 8x 4y fonksiyonunun 1 x 2 ile 1 y 1 in belirledi gi R b olgesi uzerindeki en buy uk ve en ku˘ cuk de gerini bulunuz 14) S nav notlar g(x;y;z) = 10f(x;y;z Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Show More Ex 25 Ex 25, 1F(r r ˆ)dA = Z 2ˇ 0 Zp 2 0 hx;y;z4i(r r ˆ)dˆd = Z 2ˇ 0 Z p 2 0 ˆ 2 p 2 ˆ5 8 dˆd = 2ˇ Z 2 0 ˆ2 2 p 2 ˆ5 8 dˆ = 1 3 1 6 = 1 6 1784 Use Stokes' Theorem to evaluate ZZ S curlFdS when F(x;y;z) = x2y3zi sin(xyz)j xyzk, and Sis the part of the cone y2 = x2 z2 that lies between the planes y= 0 and y= 3, oriented in the direction



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf




1 6pts Find Dz Dt When T 0 Where Z X 2 Y2 2xy X Ln T 1
Plot x^2 3y^2 z^2 = 1 Natural Language;And 4z to get x2 = y2 = z2 = 2 Since x2 y2 z2 = 3 2 = 1, we get = 2 3 and thus each of x;y;z is p1 3 You can write the Lagrangian as $$\mathcal L(x,y,z,\lambda)=x^22y^23z^2\lambda(x^2y^2z^21)$$ So we can get the gradient and putting it equal zero



Http Www Math Utoledo Edu Mtsui Calc06sp Exam Final Sol Pdf




5 Find F X F Y And F 2 Where Fx Y Z 15 10 X2 Y2 Gauthmath
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21Multiplizieren wir die ersten drei Gleichungen mit x, ybzw z




Let F X Y Z 2xy I X2 Z2 J 2yz K Check Chegg Com




Vector Analysis By Alimkanwalimtinaa Issuu
= −2y −g0(x) =⇒ g0(x) = 0 =⇒ g = const = α, say Hence f(z) = x2 −y2 2ixy iα = (xiy)2 iα = z2 iα Examples of Analytic Functions (i) f(z) = z is analytic in the whole of C Here u = x, v = y, and the Cauchy–Riemann equations are satisfied (1 = 1;X2yz=0, 2xyz=1, 3xy2z=5 \square!Factorizar x^22xyy^2 x2 2xy y2 x 2 2 x y y 2 Verificar el término medio multiplicando 2ab 2 a b y comparando el resultado con el término medio de la expresión original 2ab = 2⋅ x⋅y 2 a b = 2 ⋅ x ⋅ y Simplifica 2ab = 2xy 2 a b = 2 x y Factorizar utilizando la regla del trinomio del cuadrado perfecto, a2 2abb2 = (ab




Example 21 Factorize 4x2 Y2 Z2 4xy 2yz 4xz Examples
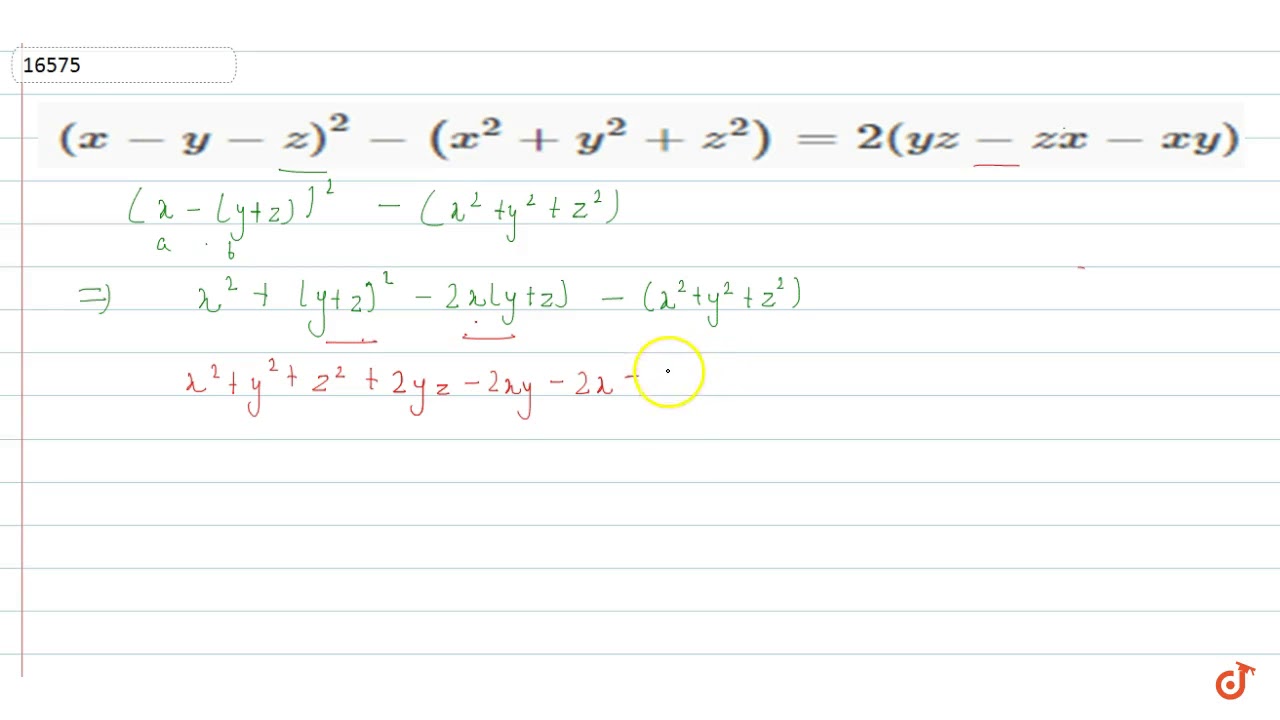



X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube
2x2yz = 1 First we rearrange the equation of the surface into the form f(x,y,z)=0 z=x^22xyy^2 x^22xyy^2z = 0 And so we define our surface function, f, by f(x,y,z) = x^22xyy^2z In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial f)/(partial y) hat(j) (partial fClick here👆to get an answer to your question ️ If the system of equations 2x y z = 0, x 2y z = 0, lambda x y 2z = 0 has infinitely many solutions and f(x) be a continuous function such that f(5 x) f(x) = 2 , then int 0^2lambdaf (x) dx is equal toQ = {(x,y) 0 ≤ x ≤ 1,0 ≤ y ≤ 1 − x} Consequently, Z C F dr = Z 1 0 Z 1−x 0 2x 4(2 − 2x − 2y) − 2y dydx = Z 1 0 Z 1−x 0 (−6x − 10y 8)dydx = Z 1 0 (x2 − 4x 3)dx = 4/3 (b) F(x,y,z) = xiy j(x2 y2)k, C is the boundary of the part of the paraboloid z = 1 − x 2− y in the first octant Solution The curl of F




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1




Important Questions And Answers Partial Differential Equations
Take the square root of both sides of the equation x^ {2}y^ {2}z^ {2}=0 Subtract z^ {2} from both sides y^ {2}x^ {2}z^ {2}=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0Math Input NEW Use textbook math notation to enter your math Try it22 Limits and continuity The absolute value measures the distance between two complex numbers Thus, z 1 and z 2 are close when jz 1 z 2jis smallWe can then de ne the limit of a complex function f(z) as follows we write



How To Eliminate The Arbitrary Function And Hence Obtain The Partial Differential Equation Z X Y F X 2 Y 2 Quora




This Makes Sense T T 2 Dt 1 T T 2 1dt 2 Du 1 3 U3 2 U 5 Pdf Free Download
Then Im(z2 1) = 2xy > 0;Συνεχίζω τα λεγόμενα του Σιλουάνου (προφανώς κ>0) Για κ=1 Η εξίσωση που προκύπτει αξίζει να μελετηθεί χωριστά!F(x;y;z) becomes a function of t Divide the equation above to get the derivative of f, df dt = f x dx dt f y dy dt f z dz dt This is an instance of the chain rule Example 111 Let f(x;y;z) = xyzz2 Suppose that x= t2, y= 3=t and z= sint Then f x= yz f y= xz and f z = 2z;




If X Y Z 0 Then Prove That X 2 Yz Y 2 Zx Z 2 Xy 3 Brainly In




Exact Equations Example 3 Video Khan Academy
0 = 0) (ii) f(z) = zn (n a positive integer) is analytic in C Here we



Multiply X2 4y2 Z2 2xy Xz 2yz By Z X 2y Studyrankersonline




Satyabama Niversity Questions In Vector




Lagrange Multipliers Ppt Download




Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And X 3 Y 3 Z 3 7 Then The Value Of X 4 Y 4 Z 4 Is




Multiply X 2 4y 2 Z 2 2xy Xz 2yz By Z X 2y




Ma2e01 Tutorial Solutions 3 1 2 Z
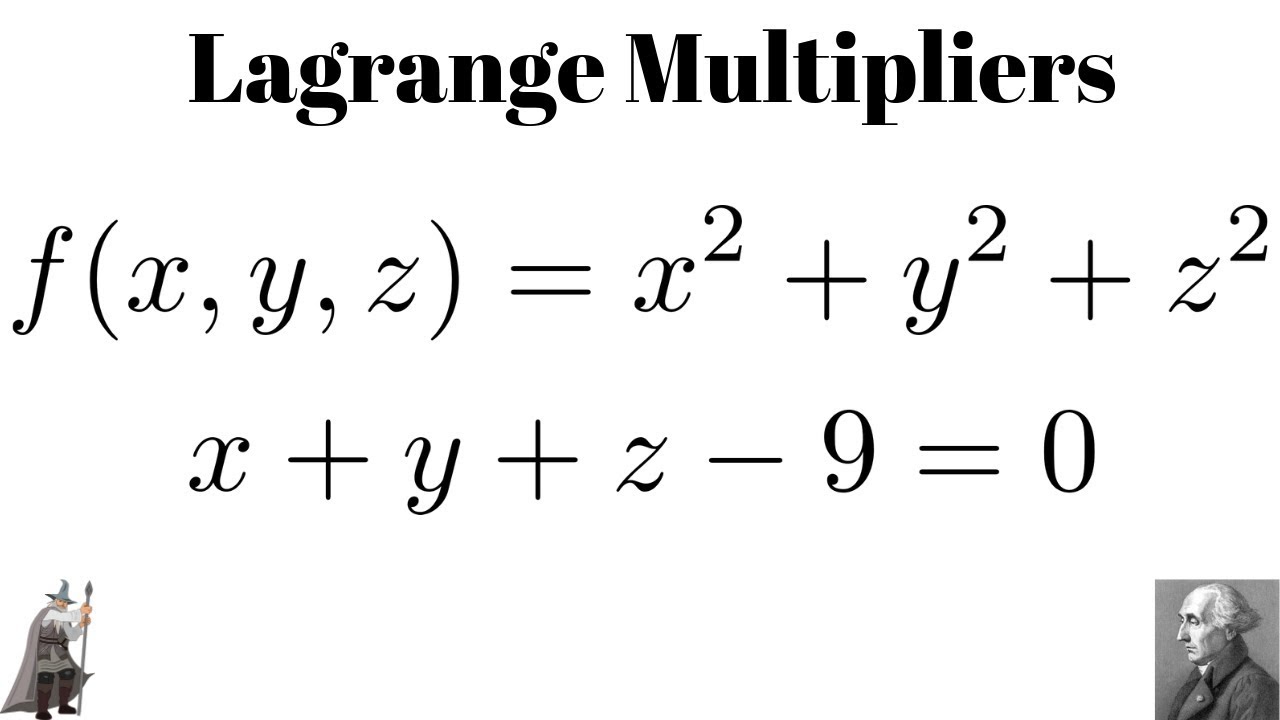



Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf



Www Math Kit Edu Iana3 Lehre Hm209s Media Hm2 06 Loe Pdf




If X Y Z 0 Then X 2 Yz Y 2 Zx Z 2 Xy Equals A 1 B 2 C 3 Brainly In




Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange




Practice Problems 10 And 11




The Surface X 2 Y 2 Z 2 2xy Z A Is Shown In The Case A 0 5 Download Scientific Diagram



Solved Solve Yz 2 X 2 Yz Dx Zx 2 Y 2 Xz Dy Xy 2 Z 2 Xy Dz 0 Subject Differential Equation And Integral Equation Course Hero




Assignment On Numerical Methods



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5



Faculty Math Illinois Edu G Choi1 242review2 Sol Pdf




Prove That U X 2 Y 2 2xy 2x 3y Is Harmonic And Find Harmonic Conjugate V Edurev Iit Jam Question




What Is The Solution To This Ode 3x 2 4xy Y 2 Dx 2x 2 2xy 9 Dy 0 Quora




This Makes Sense T T 2 Dt 1 T T 2 1dt 2 Du 1 3 U3 2 U 5 Pdf Free Download



Q Tbn And9gcq8jeckpyefv6nxxng4iwjfl7hsluh Liz05p1lqjy Usqp Cau



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community



A Show That F 2xy Z 2 I X 2j Xyzk Is A Conservative Force Field Sarthaks Econnect Largest Online Education Community



Www Math Ucla Edu Josephbreen Minimization Maximization And Lagrange Multiplier Problems Pdf




स ध द क ज ए क 2x 2 2y 2 2z 2 2xy 2yz 2zx X Y 2 Y Z 2 Z X 2




Math 6c Chapter 12 Quiz




Given F X Y Z X 2 Y X Z 4 Find F 3 5 2 Chegg Com



If X 2 Y 2 Z 2 2xyz 1 Then Prove That Dx 1 X 2 Dy 1 Y 2 Dz 1 Z 2 0 Sarthaks Econnect Largest Online Education Community



Solved Solve Yz 2 X 2 Yz Dx Zx 2 Y 2 Xz Dy Xy 2 Z 2 Xy Dz 0 Subject Differential Equation And Integral Equation Course Hero




Z 2i



1



Http Math Mit Edu Jorloff Suppnotes Suppnotes02 2s Pdf




Calculo Vectorial




Mm Prefinal Pdf Eigenvalues And Eigenvectors Matrix Mathematics




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



Www Tau Ac Il Levant Ode Solution 6 Pdf




Unit 2



70以上 Y2x2 Z2 ニスヌーピー 壁紙




Math 263 Assignment 9 Solutions 1 Find The Flux Of F X 2 Y2 K




Important Questions And Answers Partial Differential Equations



Find The Minimum Value Of X 2 Y 2 Z 2 Subject To The Conditions Xy Yz Zx 3a 2 Sarthaks Econnect Largest Online Education Community



1




Find The General Solution Of I X 2 Y 2 P 2xy Q Chegg Com




Factorise X 2 Y 2 Z 2 2xy 2xz 2yz Brainly In




X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy




Answered 14 F X Y Z X Y 4z X Y Bartleby




70以上 Y2x2 Z2 ニスヌーピー 壁紙



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Hw2sol



How To Create A Partial Differential Equation By Eliminating Arbitrary Function F And G From Z F X 2y G 2x Y Quora




Partial Differential Equations



Http Web Iitd Ac In Rksharma Mtl 100 webpage Tutsheet5 Pdf




F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com



Www Ualberta Ca Rjia Math214 Hwks Sol8 Pdf




Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y




Find The Point S On The Surface At Which The Tangent Chegg Com




Vector Analysis By Alimkanwalimtinaa Issuu




How To Do Implicit Differentiation 7 Steps With Pictures




Describe The Domain Of The Function F In Words A Chegg Com




For F X Y X 2 Y 2 2xy Sketch F A For X 0 Mathematics Stack Exchange




Partial Differential Equations




Verify That X Y Z 2 X 2 Y 2 Z 2 2xy 2yz 2zx




Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



Solved Find The Integral Surface Of The Partial Differential Equation 2xy 1 P Z 2x3 Q 2 X Yz Through Curves X 1 And Y 0 Course Hero



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam4f16 Pdf



Curl Of A Vector Field Compute The Curl Of The Chegg Com



0 件のコメント:
コメントを投稿