はじめに 因数分解とは、「足し算・引き算で表されている数式をかけ算の形に変形する」ことです。 数学の色んな場面で出てきます。 そんな因数分解には、公式だけでなく早く計算できる解き方があります。 今回の記事では、「因数分解とは何か?」という基礎的な内容から、解き方の解説や練習問題まで載せています。将5 1985 1 分解成为3个因数相乘 要求每一个因数都大于5 100 平静地 Csdn博客如果数学好,相信这个代码不会难。 在本例子中,输入90,打印出90=2*3*3*5。 解 题 思路和方法:对n 分解质因数 ,需要先找到一个最小的质数k,然后按下述步骤完成: (1)如果这个质数恰等于n,则说明 分解质因数 的过程已经结束,打印出即可。 (2)如果n <>

高校数学 数 10 因数分解 応用編 Youtube
数1 因数分解 交代式
数1 因数分解 交代式-分解とは、1つにまとまっているものをいくつかのものに分けることです。 ですので、この、因数分解という言葉は簡単にまとめてしまえば、式を展開することの逆バージョンであるといえます。 例えば、15という数は、 3×5;因数分解とは 因数分解とは、1 つの整式を複数の整式の積に変形する操作をいいます。 変形後の積をなすもののそれぞれを因数と呼びます。 ※整式:単項式と多項式を合わせたもの。 例えば次の例を見てみましょう。 これは最も簡単な因数分解の 1 つです。 pa qa という整式が、p q という整式と a という整式の掛け算に変形されています。 先ほど




怎么对一个数字进行因式分解 最有妙招网
残念ながらこれらの公式は 因数分解 で使うため全て覚える必要があるのですが、こと展開計算に関しては、むしろ公式を使わない汎用的な解法を使った方が早いし正確と言えます。 問1 以下の式を展開しなさい。 将来の大学受験を見据えると、公式を数1因数分解 たすき掛け整数分解工具计算一个给定的自然数的质因数,也可以使用带 * / ^ !分 解质 因数 bai 的方法有 du 两种 : 1、相 乘法 写成几个质 zhi 数相乘的 dao 形式(这些不 版 重 复的 质数即 为质 权 因数),实际运算时可采用逐步分解的方式。 如:36=2*2*3*3 运算时可逐步分解写成36=4*9=2*2*3*3或3*12=3*2*2*3 2、短除法 从最小的质数除起,一直除到结果为质数为止素因数分解 (そいんすうぶんかい、英 prime factorization) とは、ある正の整数を素数の積の形で表すことである。 ただし、1 に対する素因数分解は 1 と定義する 。 素因数分解には次のような性質がある。 任意の正の整数に対して、素因数分解はただ 1 通りに決定する(素因数分解の一意性)。
因数分解(基本問題1) 次の式を因数分解しなさい x 2 4x 4x 22x axay x 2 3x2 x 2 6x5 x 2 12x 次の式を因数分解しなさい x 2 7x10 x 2 11x10 x 211x30 x 213x42 x 26x9 次の式を因数分解しなさい x 2 2x35 x 2 x30 x 2 3x40 x 2 18x81 x 29 x 216新しい 数 1 因数 分解 X N 1 的因式分解 代数 包括初等代数 数项级数 代数不等式 约数个数问题的常规解法 18年11月19日 知乎念頭におき,本論文では整式xn-1の因数分解は基 本的に「有理数体上で」考えるものとする。 なお,有理数体で整式xn-1の因数分解を考える 上で,その既約多項式の既約性が問題となる。岩永 (02)は,「既約多項式は多項式環において,重要な
因数分解の公式は、中学3年生で学習するものは、以下の通りです。 a2+2ab+b2= (a+b)2 a2-2ab+b2= (a-b)2 x2+ (a+b)x+ab= (x+a) (x+b) a2-b2= (a+b) (a-b) 高校1年、つまり数Ⅰで新しく学習するものは、 acx2+ (ad+bc)x+bd= (ax+b) (cx+d) いわゆる§1 数 と 式 1 因数分解 5ab 2 のように,いくつかの文字や数を掛け合わせてできる式を単項式といい,また,4x 2 6x7のように,いくつかの単項式の和として表される式を,多項式という。 単項式と,多項式をあわせて整式と呼び,次数がnの整式をn次式という。因数分解は 1.共通因数でくくる 2.公式の利用 が基本です。 しかし、公式利用の中でも acx^2 (adbc)xcd= (axb) (cxd) この公式を利用した因数分解は複雑で暗算では 数学Ⅰ 数と式 因数分解の基本手順 問 次の式を因数分解せよ (1) 9x^ {2}y^ {2}6xy^3 (2) a (xy
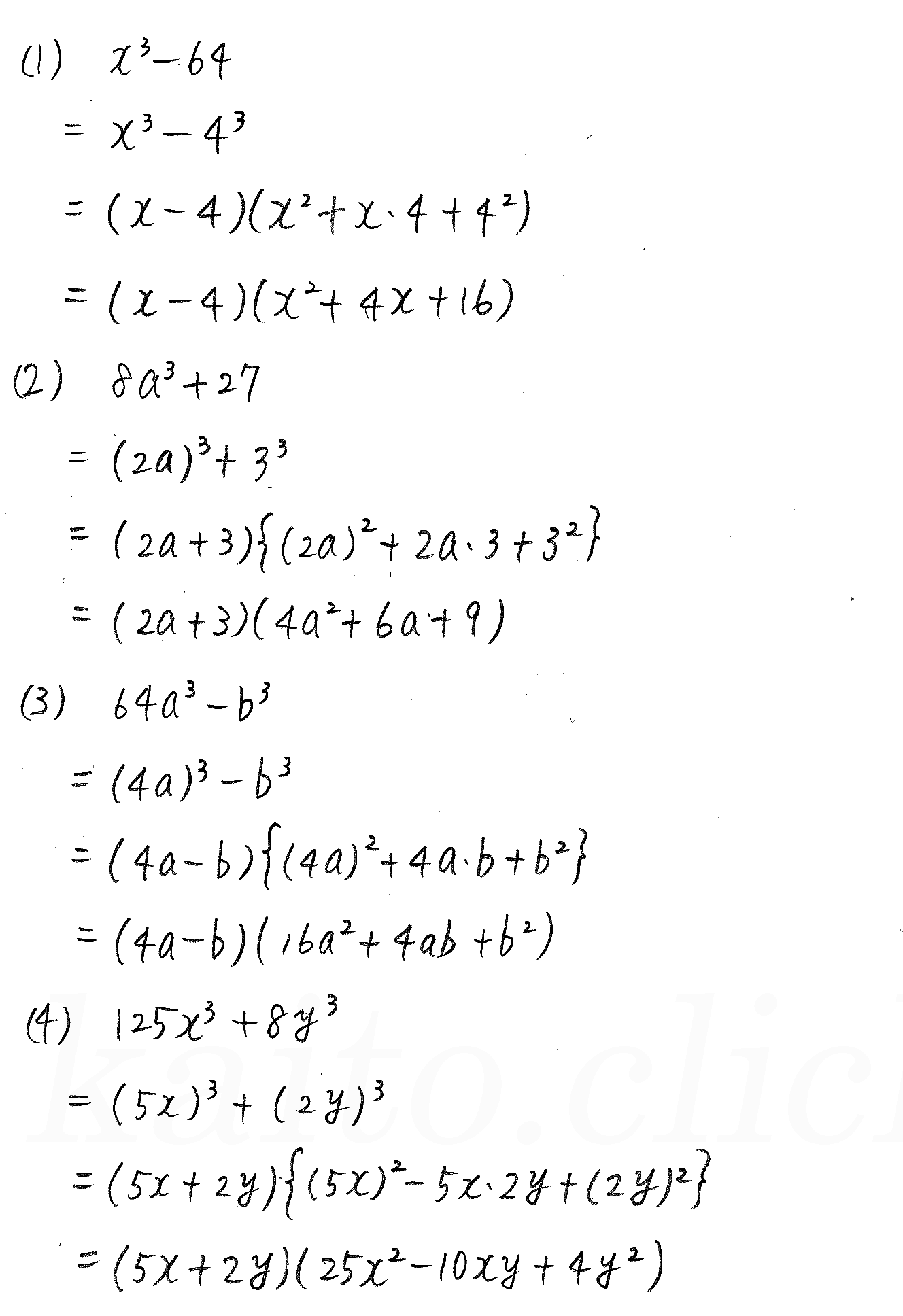



改訂版 3trial数学 P14 3 因数分解 練習問題
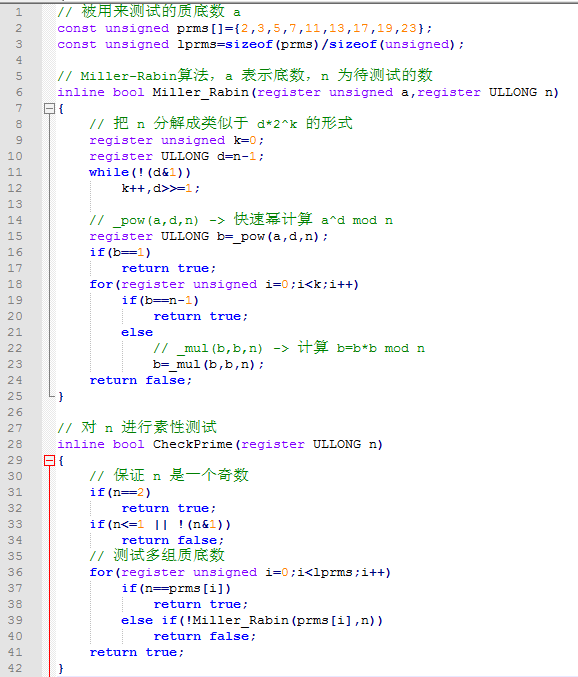



研学 质因数分解及素性判定 Mnihyc S Blog
数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。若一个大于1正整数n可以分解质因数:n=(p1^a1)*(p2^a2)*(p3^a3)**(pk^ak), 则由约数个数定理可知n的正约数有 (a11)(a21)(a31)(ak1)个。 本题要求一个给定丑数n的约数个数,而一个丑数分解质因数后,其质因子只有2、3、5或7这4个,因此只需求出n中分别含有质因子2、3、5和7的个をたすき掛けを使って因数分解せよ。 解答&解説 x 2 の係数は1、定数項は3です。 掛け合わせて1になるのは「1と1」、「1と1」 掛け合わせて3になるのは「1と3」、「1と3」 ですね。たすき掛けがうまくいくのは以下の組み合わせです。




互质是什么意思 又叫互素 真问网




怎么找最大公因数 生活百科
質問: 高校数字Ⅰ因数分解です。 黄色のマーカー部分がよく分かりません。 tamu 先生の回答 マーカー1行目から2行目は共通因数(bc)でくくっています。 マーカー2行目から3行目は因数分解 x^2(ab この質問・回答を見るA1 <= a2 <= a3 <= <= an,问这样的 分解 的种数有多少。 注意到a = a也是一种 分解 。 Input 第1行是测试数据的组数n,后面跟着n行输入。 每组测试数据占1行,包括一个正整数a (1 <因数分解1 数 と式 式の




怎样快速求出一个数的因数的个数




因式分解 易错点辨析 参考网
高1 数1 因数分解(対称式と交代式) 高校生 数学のノート Clear 表紙 1 2 公開日時 21年03月05日 10時28分 更新日時 21年03月05日 12時43分 高校生 1年生 数学数と式:因数分解: 因数分解 (a^2b^2c^2−3abc)の形のもの 数学、物理、化学の勉強やりなおします~挫折した皆さんとともに~整数分解工具 整数分解工具 计算一个给定的自然数的质因数,也可以使用带 * / ^ !




72的因数分解个数 72的因数有哪些 三人行教育网 Www 3rxing Org



Studydoctor3乗の因数分解 数 Studydoctor
おきかえを使った因数分解 式の中の共通な部分を 他の文字におきかえて 因数分解する。 例1 9x 26x1 3x =Aとおくと 9x 26x1 = A 22A1 = (A1) 2 = (3x1) 2 例2 16x 29y 2 4x=A, 3y=Bと的表达式。 分解结果将以递增的质因数乘积形式展示。 如果您的表达式为质数,结果将为该数本身。 如果需要检测一个数是否为质数,您应当使用 Prime Number Calculator (质数发生器和校验器),其支持更大的的数。 支持的函数和运算C语言编程统计 因数分解 的种数 0102 给出一个正整数a,要求 分解 成若干个正整数的乘积,即a = a1 * a2 * a3 * * an,并且1 <




Rsa 理论的正向思考过程 二 Yui 的严肃文
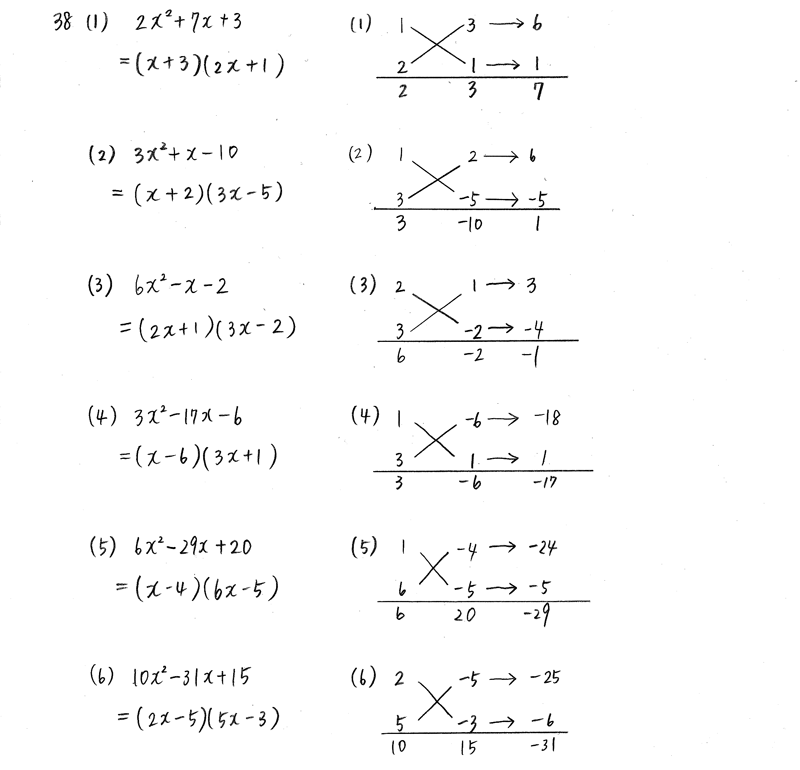



クリアー数学 数1 P13 4 因数分解 1
適当な公式を用いて,次の式を因数分解せよ。 \ 10 次の式を因数分解せよ。 de d e de de d e \ de\ 11 次の式を因数分解せよ。 数学Ⅰ 数と式(因数分解) 演習プリント3 = 6不去相信,次数1和2又怎么能变成6呢? 事实上的结论是:(1 1)×(2 1)= 6个。 即某一自然数的约数个数是它各质因数的次数分别加1相乘的积!!! 那么,根据上述结论, 我们将180进行分解,具体如下:工夫をして因数分解を行う問題 式を因数分解するときに、ちょっと工夫をすることで楽に因数分解ができるようになります。練習問題を解きながら、楽に因数分解ができる方法を身につけていきましょう。 練習問題 問題 次の式を因数分解せよ (1) x²-9y²




数学 大数质因数分解定理 M0 的博客 Csdn博客 大质数分解




如何对二项式进行因式分解 包含图片
因数分解 (18) 数1 (46) 数と式 (42) 整式の加法・減法・乗法 (24) 場合の数 (2) 集合の要素の個数 (2) 組合せ (2) 雑談 (1) はてなブログをはじめよう! n9h28eg0因子、乗法因子、乗因子)と呼ばれる—の積として書き表すことを言う注釈 2。たとえば、15 という数は 3 ×因数分解Q&A No 因数分解ってなんですか。 No 1次式も因数分解しないとダメですか。 No ax2bxc a x 2 b x c を因数分解するにはどうすればよいですか。 No 因数分解せよと言われて 2x26x4 =(2x2)(x2) 2 x 2 6 x 4 = ( 2 x 2) ( x 2) と




35的因数35分解质因数35如何分解质因数




怎么对一个数字进行因式分解 最有妙招网
因数分解は 1.共通因数でくくる 2.公式の利用 が基本です。 しかし、公式利用の中でも \(acx^2(adbc)xcd=(axb)(cxd)\) この公式を利用した因数分解は複雑で暗算では動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaruそこで役に立つのが、この「因数分解」という考え方です。 アパレルショップの売上を「因数」で分解してみましょう。 お店の売上=購入してくれるお客様の数×客単価 と表すことができます。 つまり売上を上げようと思ったら、購入してくれたお客様の数を増やすか、客単価を上げるか、その2つの方法がある、と考えることができます。 さらにこれを細かく
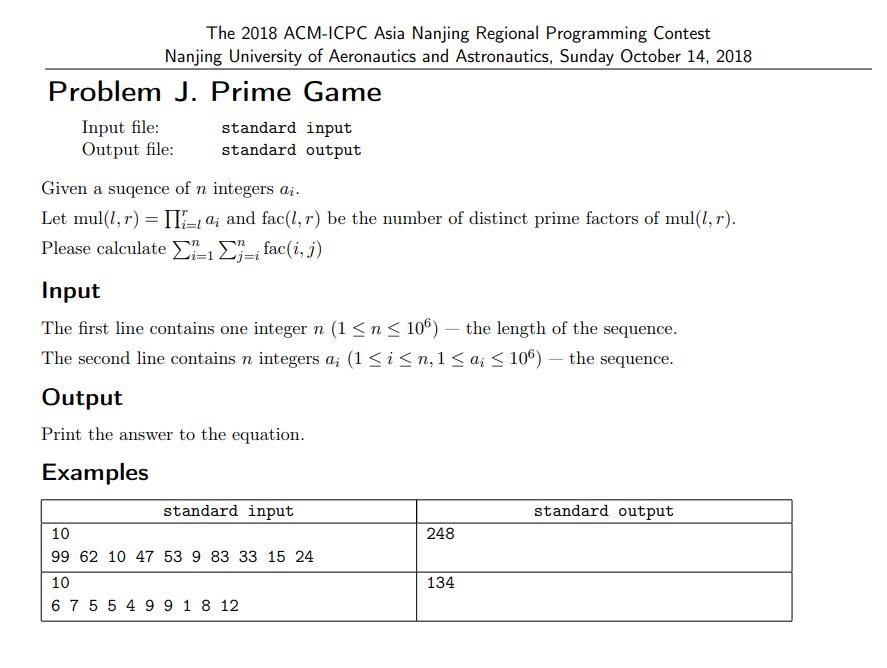



Prime Game 质因数分解 线性筛 思维 Xxiaoyu 博客园



大因数分解 Pollard Rho算法 Leflacon S Blog
数学における因数分解(いんすうぶんかい、英 factorization, factoring, decomposition注釈 1;このノートについて 미유리 高校1年生 高校1年生の最初にやる内容です。 例題も基本的なものから応用まで書いたのでやってみて下さい! 数1 式の計算 展開 因数分解 たすき掛け 数一 数1 数Ⅰ このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます!高校数学の要点, 無料の練習問題, 例題と解説 因数分解1 Menu 高校数学学習サイト 更新日 TOP >




牛客多校 第四场 B Basic Gcd Problem 质因数分解 程序员大本营




数学 質問解答 4乗 を含んだ因数分解 パート1 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生
この記事では「(1)因数分解を使うタイプ」の問題について紹介していきたいと思います。 整数問題を因数分解を使って解く 例題$\ n\ $が2以上の素数でない整数ならば、$\ 2^n1\ $も素数でないことを示せ。1次式の因数分解は,共通因数でくくる変形があるだけですから,共通因数を考えます. (ab) x (ab)(a−b) =(ab)(xa−b) (答)1、如果这个质数恰等于n,则说明分解质因数的过程已经结束,打印出即可。 2、如果n!=k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数你n,重复执行第一步。 3、如果n不能被k整除,则用k1作为k的值,重复执行第一步。 代码实现:




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




高校数学 数 10 因数分解 応用編 Youtube
因数分解是将一个正整数写成几个约数的乘积,在代数学、密码学、计算复杂性理论和量子计算机等领域中有重要意义 1 。 因数分解的关键是寻找因子(约数),而完整的 因子 列表可以根据约数分解推导出,将 幂 从零不断增加直到等于这个数。



1




高校数学 数 11 因数分解 3次式の公式編 Youtube




质因数分解与量子计算机 知乎




19 1 18 初一数学质因数分解大法1 质数2 从小到大 Site Engineer 工作日志 Facebook




怎么对一个数字进行因式分解 最有妙招网




题目出错 多种答案 唯一答案 质数 分解质因数重要性质和应用 每日头条




质因数分解 Blackvvv 的博客 Csdn博客



脳トレ数学 因数分解 展開 安卓下载 安卓版apk 免费下载




约数个数问题的常规解法 18年11月19日 知乎
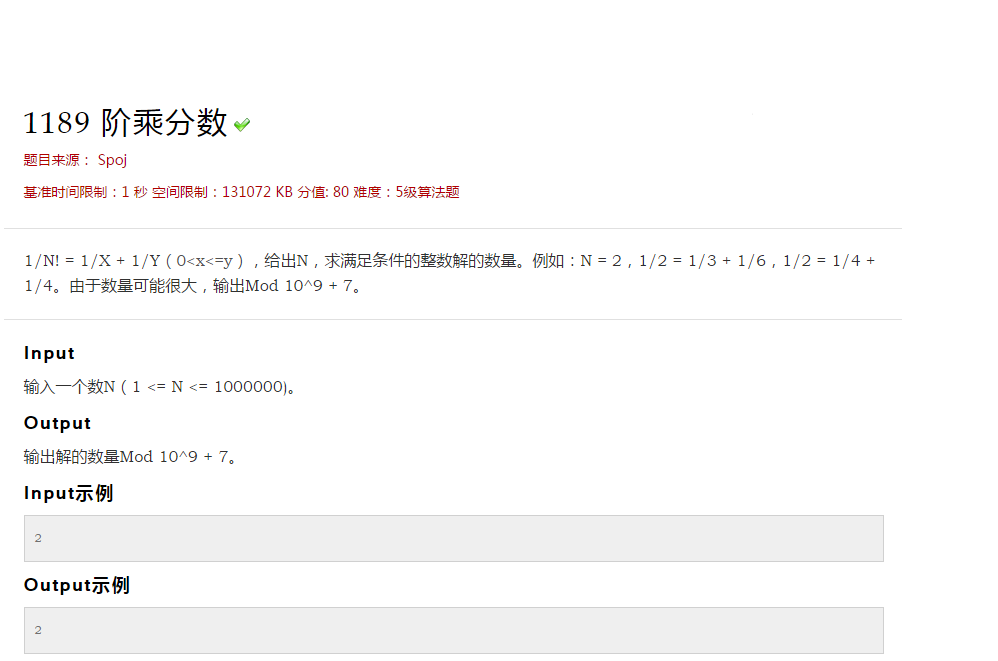



51nod 11 阶乘分数 阶乘质因数分解 Child Single 博客园




数検1級対策 1次 因数分解 因数分解 数検1級1次問題
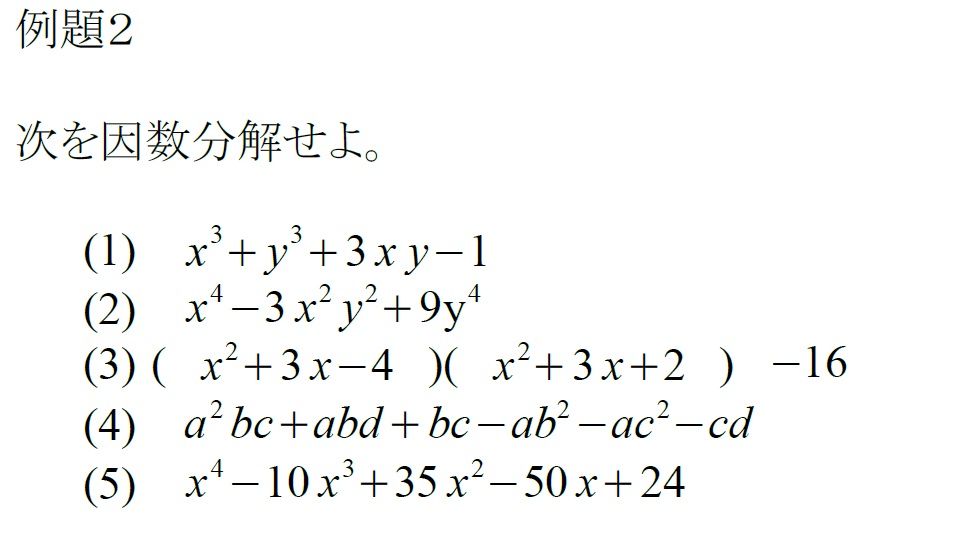



鉄則2 数と式 因数分解 寺田の数学合格鉄則96に関するメモ




数1 因数分解 の問題です この問題 3行目マーカーの Y Z は Clear




因数分解難問と意外な別解 怜悧玲瓏 高校数学を天空から俯瞰する



分解素因数的方法 百度经验



因数分解 腾讯视频




质因数分解及代码 Youxin 博客园



初中数学基础 因式分解中的符号问题 没学好的学生抓紧来学




2 29 541 7919 素数 整数 合数 质数 因数 网易订阅



1到100质数表 100以内的质数图片 质数表口诀 最全知识分享




夏まとめ 数学1 因数分解 高校生 数学のノート Clear




整理1 最小和数 整数质因数分解 不吃黑巧克力也能活的博客 Csdn博客




衝撃の解答 数検1級の公式解答も間違ってた伝説の因数分解がヤバすぎた Youtube



高校数学 数 8 因数分解 基本編 Youtube




算法讲解 质数判断及质因数分解 阿维斯托 博客园



免费计算器 附质因数分解功能 安卓下载 安卓版apk 免费下载
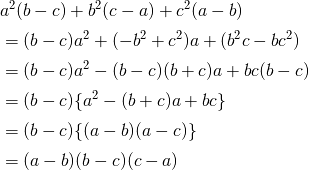



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局



高校数学 数1の因数分解について質問です 画像の問題の Yahoo 知恵袋




质因数 分解质因数ppt精选文档下载 Ppt模板 爱问共享资料




Lcp 14 切分数组




聊聊素数 与孪生素数 知乎




因数分解の公式まとめ一覧とその活用例 アタリマエ




高校入試 因数分解の難問を解説 難関高校の入試問題に挑戦しよう 数スタ



1




例題 利用質因數分解找出一個數所有的因數練習 數學 均一教育平台




质因数能分解出的最高个数 代号4101的专栏 Csdn博客
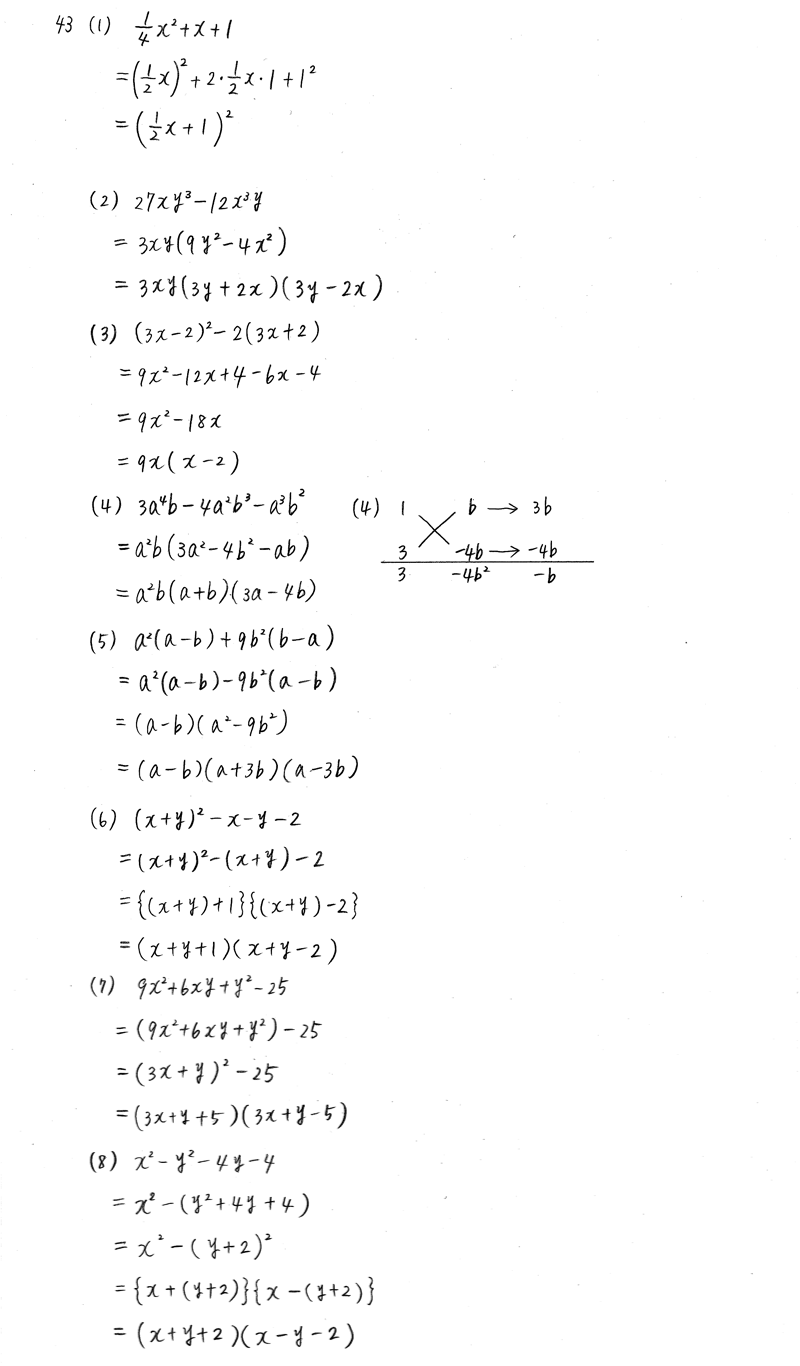



クリアー数学 数1 P14 5 因数分解 2




因式分解之待定係數法 一元三次多項式分解 每日頭條




國三junior High数学的 中3 数学 因数分解 式の計算の利用筆記 Clear




如何因式分解三次多项式 12 步骤
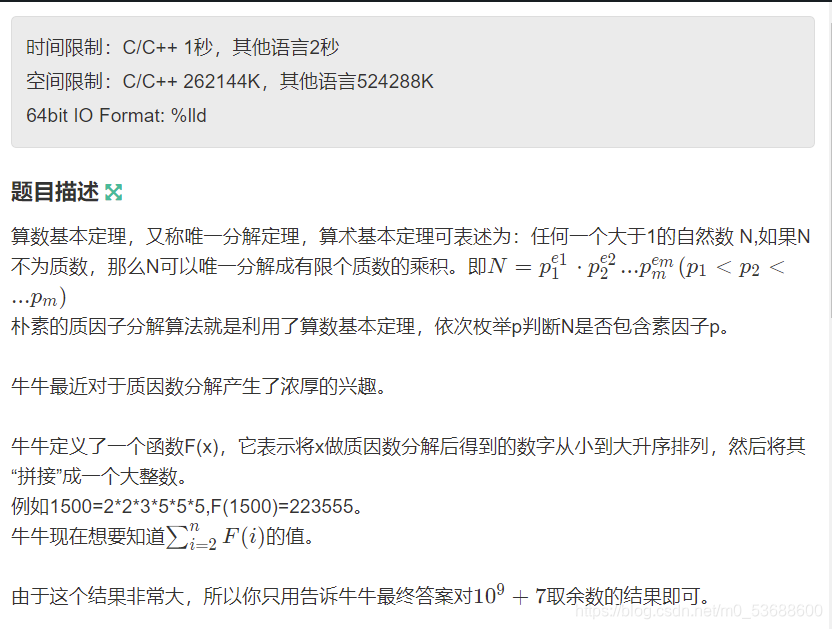



牛牛的质因数 M0 的博客 Csdn博客




因数分解で必要な公式を集めてみました 高校数学の達人 河見賢司の日記
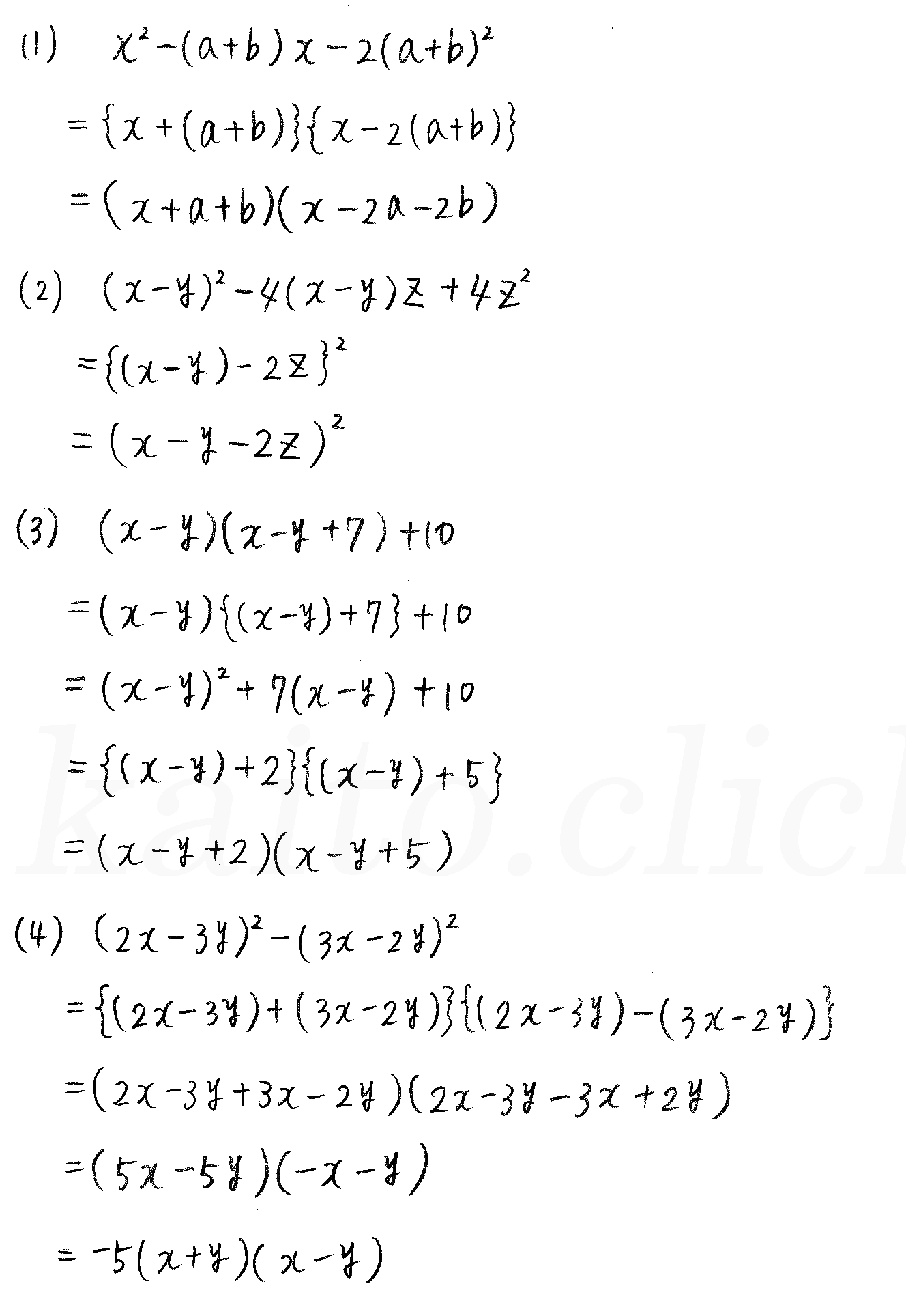



改訂版 クリアー数学 P15 5 因数分解 2




怎么对一个数字进行因式分解 最有妙招网




初中数学 初一数学 因式分解 练习题 精选 Doc 蚂蚁文库



Studydoctor平方の差を利用する因数分解 数 Studydoctor




浙江事业单位考试 质因数分解
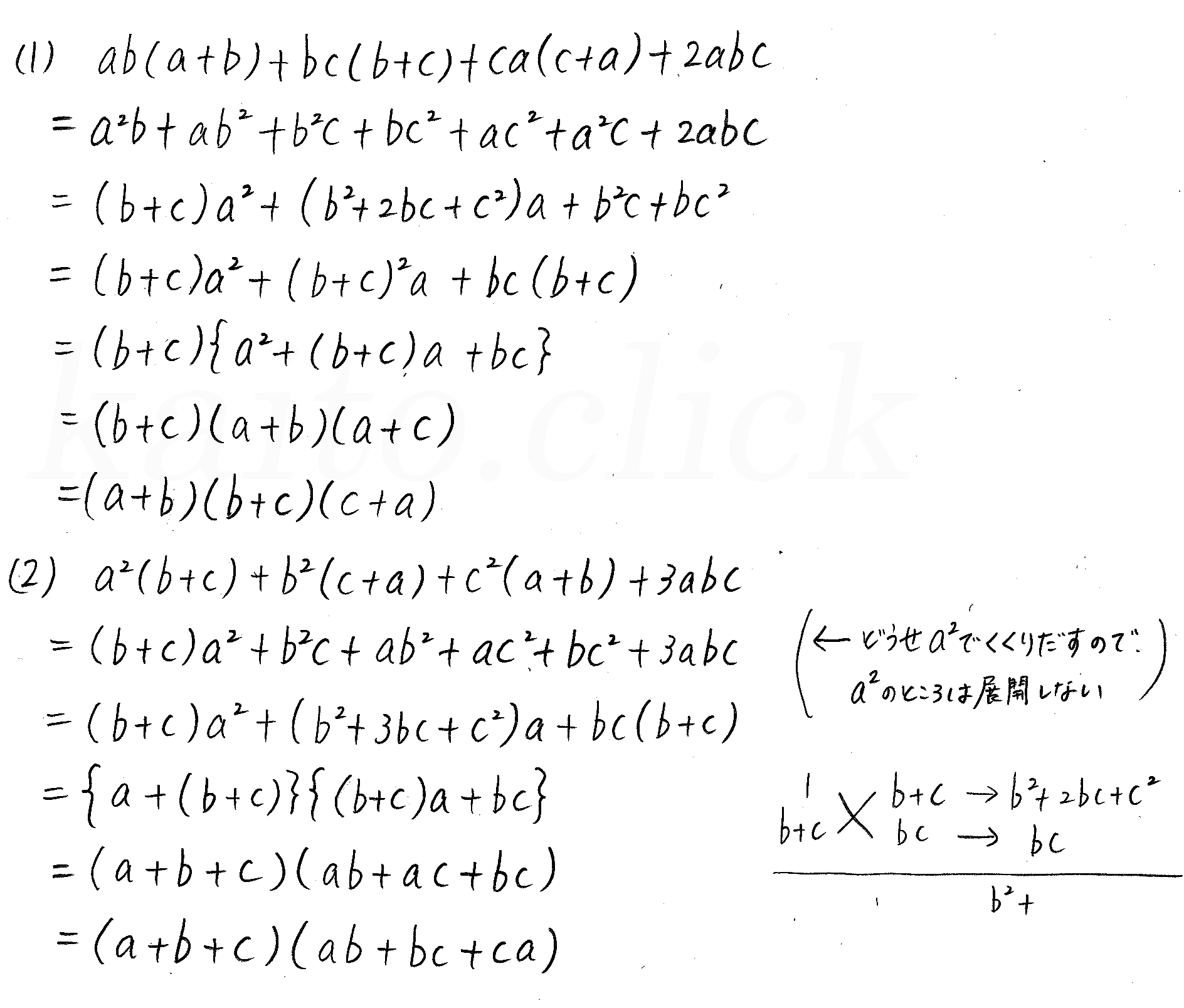



改訂版 3trial数学 P13 3 因数分解




什么是分解质因数 分解质因数的方法例子 豪友网



分解质因数是什么 初三网



河野玄斗 冲击的答案 数检1级的公式答案也是错误的传说的因数分解太可怕了 哔哩哔哩 つロ干杯 Bilibili




高校数学 因数分解の工夫 置き換え 受験の月
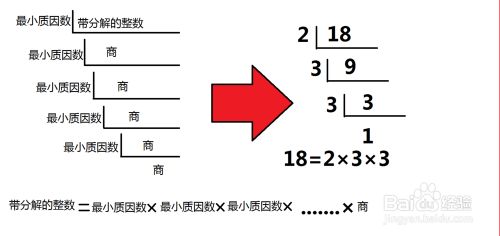



分解素因数的方法 百度经验
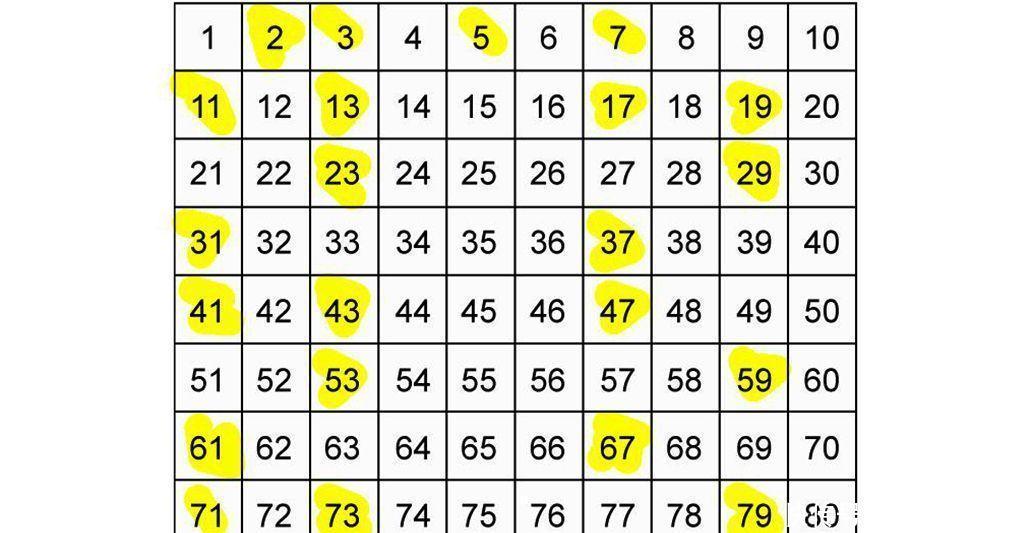



将25分解成质因数




この赤枠のようになる理屈がわかりません 詳しく教えて頂きたいです Clear




Python 因式分解 10 分 W的博客 程序员宅基地 Python因式分解 程序员宅基地



因数分解 腾讯视频




すごい因数分解 Amazing Factorization Youtube




怎么对一个数字进行因式分解 最有妙招网



大因数分解 Pollard Rho算法 Leflacon S Blog



质因数分解 标签 Oier博客



1到100的因数表图片 万图壁纸网




数i 難しい因数分解 整理しなおす問題 Youtube



3



121分解质因数分解质因数 1 52 2 68 3 121 数学 魔方格




如何分解因式 搜狗指南




如何因式分解三次多项式 12 步骤




Hpu暑期第五次积分赛f 辞树的质因数分解 牛客博客



质因数 知乎



悟空问答 18的因数有几个 14个回答




展開 因数分解は1時間で解けるようになる 外資系コンサルタントが主夫になったら
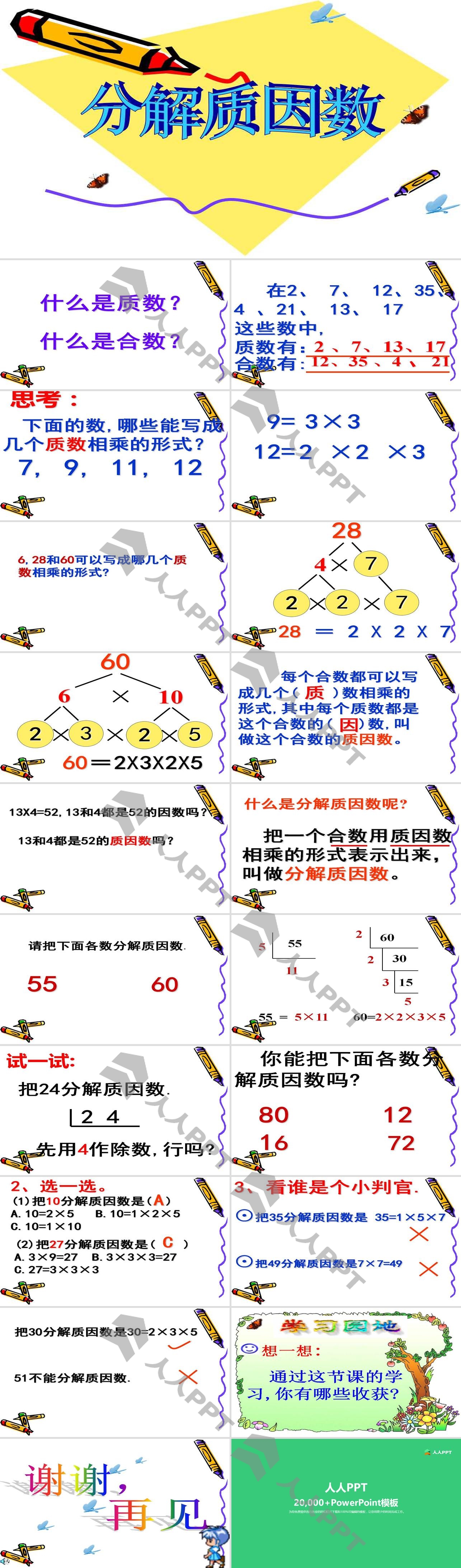



分解质因数 因数和倍数ppt课件 Ppt课件下载 人人ppt




怎么对一个数字进行因式分解 最有妙招网




P1075 Noip12 普及组 质因数分解 在 为什么不学习的博客 Csdn博客



Search Q E5 9b A0 E5 8f E5 86 E8 A3 E8 8b B1 E6 96 87 Tbm Isch



大数的质因数分解 西瓜视频搜索




10 5 因式分解 Ppt Download




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ
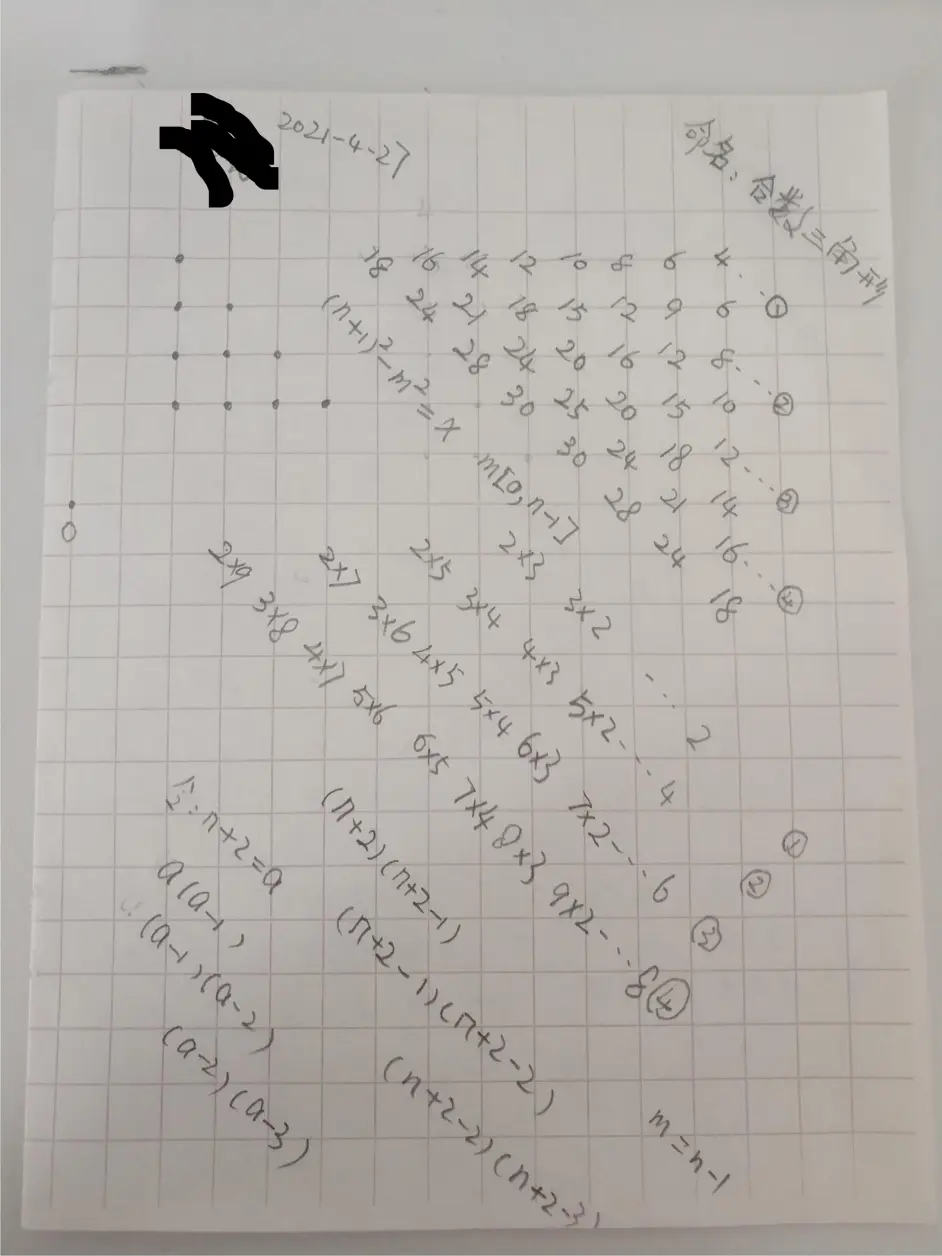



数字1 既不是质数也不是合数的几何证明 合数三角形 N Pq的分解公式 哔哩哔哩




中3 展開と因数分解13 公式を使う因数分解1 予習 中学数学の勉強に




中考数学 50道经典因式分解详解例题 知乎



25的全部因数 西瓜视频搜索



质因数分解 Kkxxzx的博客 程序员宅基地 程序员宅基地



质因数分解下载 Word模板 爱问共享资料



0 件のコメント:
コメントを投稿